A tangent is a straight line , which touches the graph of the function at one point and all points of which are at the shortest distance from the graph of the function. Therefore, the tangent passes tangent to the graph of the function at a certain angle and several tangents at a certain angle cannot pass through the point of tangency. different angles. Tangent equations and normal equations to the graph of a function are constructed using the derivative.
The tangent equation is derived from the line equation .
Let us derive the equation of the tangent, and then the equation of the normal to the graph of the function.
y = kx + b .
In it k - slope.
From here we get the following entry:
y - y 0 = k(x - x 0 ) .
Derivative value f "(x 0 ) functions y = f(x) at the point x0 equal to the slope k= tg φ tangent to the graph of a function drawn through a point M0 (x 0 , y 0 ) , Where y0 = f(x 0 ) . This is geometric meaning derivative .
Thus, we can replace k on f "(x 0 ) and get the following equation of the tangent to the graph of a function :
y - y 0 = f "(x 0 )(x - x 0 ) .
In problems involving composing the equation of a tangent to the graph of a function (and we will move on to them soon), it is required to reduce the equation obtained from the above formula to equation of a straight line in general form. To do this, you need to move all the letters and numbers to the left side of the equation, and leave zero on the right side.
Now about the normal equation. Normal - this is a straight line passing through the point of tangency to the graph of the function perpendicular to the tangent. Normal equation :
(x - x 0 ) + f "(x 0 )(y - y 0 ) = 0
To warm up, you are asked to solve the first example yourself, and then look at the solution. There is every reason to hope that this task will not be a “cold shower” for our readers.
Example 0. Create a tangent equation and a normal equation for the graph of a function at a point M (1, 1) .
Example 1. Write a tangent equation and a normal equation for the graph of a function ![]() , if the abscissa is tangent .
, if the abscissa is tangent .
Let's find the derivative of the function:
Now we have everything that needs to be substituted into the entry given in the theoretical help to get the tangent equation. We get
![]()
In this example, we were lucky: the slope turned out to be zero, so we separately reduce the equation to general appearance wasn't needed. Now we can create the normal equation:
![]()
In the figure below: graph of a function burgundy color, tangent green, orange normal.

The next example is also not complicated: the function, as in the previous one, is also a polynomial, but the slope will not be equal to zero, so one more step will be added - bringing the equation to a general form.
Example 2.
Solution. Let's find the ordinate of the tangent point:
Let's find the derivative of the function:
![]() .
.
Let's find the value of the derivative at the point of tangency, that is, the slope of the tangent:
We substitute all the obtained data into the “blank formula” and get the tangent equation:
![]()
We bring the equation to its general form (we collect all letters and numbers other than zero on the left side, and leave zero on the right):
We compose the normal equation:

Example 3. Write the equation of the tangent and the equation of the normal to the graph of the function if the abscissa is the point of tangency.
Solution. Let's find the ordinate of the tangent point:
Let's find the derivative of the function:
![]() .
.
Let's find the value of the derivative at the point of tangency, that is, the slope of the tangent:
![]() .
.
We find the tangent equation:
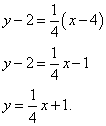
Before bringing the equation to its general form, you need to “comb it” a little: multiply term by term by 4. We do this and bring the equation to its general form:
We compose the normal equation:
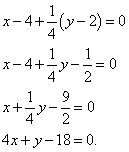
Example 4. Write the equation of the tangent and the equation of the normal to the graph of the function if the abscissa is the point of tangency.
Solution. Let's find the ordinate of the tangent point:
![]() .
.
Let's find the derivative of the function:
Let's find the value of the derivative at the point of tangency, that is, the slope of the tangent:
![]() .
.
We get the tangent equation:
We bring the equation to its general form:
We compose the normal equation:
![]()
A common mistake when writing tangent and normal equations is not to notice that the function given in the example is complex and to calculate its derivative as the derivative of a simple function. The following examples are already from complex functions(the corresponding lesson will open in a new window).
Example 5. Write the equation of the tangent and the equation of the normal to the graph of the function if the abscissa is the point of tangency.
Solution. Let's find the ordinate of the tangent point:
Attention! This function- complex, since the tangent argument (2 x) is itself a function. Therefore, we find the derivative of a function as the derivative of a complex function.
Instructions
We determine the angular coefficient of the tangent to the curve at point M.
The curve representing the graph of the function y = f(x) is continuous in a certain neighborhood of the point M (including the point M itself).
If the value f‘(x0) does not exist, then either there is no tangent, or it runs vertically. In view of this, the presence of a derivative of the function at the point x0 is due to the existence of a non-vertical tangent tangent to the graph of the function at the point (x0, f(x0)). In this case, the angular coefficient of the tangent will be equal to f "(x0). Thus, the geometric meaning of the derivative becomes clear - the calculation of the angular coefficient of the tangent.
Find the abscissa value of the tangent point, which is denoted by the letter “a”. If it coincides with a given tangent point, then "a" will be its x-coordinate. Determine the value functions f(a) by substituting into the equation functions abscissa value.
Determine the first derivative of the equation functions f’(x) and substitute the value of point “a” into it.
Take general equation tangent, which is defined as y = f(a) = f (a)(x – a), and substitute the found values of a, f(a), f "(a) into it. As a result, the solution to the graph and the tangent will be found.
Solve the problem in a different way if the given tangent point does not coincide with the tangent point. In this case, it is necessary to substitute “a” instead of numbers in the tangent equation. After this, instead of the letters “x” and “y”, substitute the value of the coordinates of the given point. Solve the resulting equation in which “a” is the unknown. Plug the resulting value into the tangent equation.
Write an equation for a tangent with the letter “a” if the problem statement specifies the equation functions and the equation of a parallel line relative to the desired tangent. After this we need the derivative functions, to the coordinate at point “a”. Substitute the appropriate value into the tangent equation and solve the function.
Example 1. Given a function f(x) = 3x 2 + 4x– 5. Let’s write the equation of the tangent to the graph of the function f(x) at the graph point with the abscissa x 0 = 1.
Solution. Derivative of a function f(x) exists for any x R . Let's find her:
= (3x 2 + 4x– 5)′ = 6 x + 4.
Then f(x 0) = f(1) = 2; (x 0) = = 10. The tangent equation has the form:
y = (x 0) (x – x 0) + f(x 0),
y = 10(x – 1) + 2,
y = 10x – 8.
Answer. y = 10x – 8.
Example 2. Given a function f(x) = x 3 – 3x 2 + 2x+ 5. Let's write the equation of the tangent to the graph of the function f(x), parallel to the line y = 2x – 11.
Solution. Derivative of a function f(x) exists for any x R . Let's find her:
= (x 3 – 3x 2 + 2x+ 5)′ = 3 x 2 – 6x + 2.
Since the tangent to the graph of the function f(x) at the abscissa point x 0 is parallel to the line y = 2x– 11, then its slope is equal to 2, i.e. ( x 0) = 2. Let’s find this abscissa from the condition that 3 x– 6x 0 + 2 = 2. This equality is valid only when x 0 = 0 and at x 0 = 2. Since in both cases f(x 0) = 5, then straight y = 2x + b touches the graph of the function either at the point (0; 5) or at the point (2; 5).
In the first case, the numerical equality 5 = 2×0 + is true b, where b= 5, and in the second case the numerical equality 5 = 2×2 + is true b, where b = 1.
So there are two tangents y = 2x+ 5 and y = 2x+ 1 to the graph of the function f(x), parallel to the line y = 2x – 11.
Answer. y = 2x + 5, y = 2x + 1.
Example 3. Given a function f(x) = x 2 – 6x+ 7. Let’s write the equation of the tangent to the graph of the function f(x), passing through the point A (2; –5).
Solution. Because f(2) –5, then point A does not belong to the graph of the function f(x). Let x 0 - abscissa of the tangent point.
Derivative of a function f(x) exists for any x R . Let's find her:
= (x 2 – 6x+ 1)′ = 2 x – 6.
Then f(x 0) = x– 6x 0 + 7; (x 0) = 2x 0 – 6. The tangent equation has the form:
y = (2x 0 – 6)(x – x 0) + x– 6x+ 7,
y = (2x 0 – 6)x– x+ 7.
Since the point A belongs to the tangent, then the numerical equality is true
–5 = (2x 0 – 6)×2– x+ 7,
where x 0 = 0 or x 0 = 4. This means that through the point A you can draw two tangents to the graph of the function f(x).
If x 0 = 0, then the tangent equation has the form y = –6x+ 7. If x 0 = 4, then the tangent equation has the form y = 2x – 9.
Answer. y = –6x + 7, y = 2x – 9.
Example 4. Functions given f(x) = x 2 – 2x+ 2 and g(x) = –x 2 – 3. Let’s write the equation of the common tangent to the graphs of these functions.
Solution. Let x 1 - abscissa of the point of tangency of the desired line with the graph of the function f(x), A x 2 - abscissa of the point of tangency of the same line with the graph of the function g(x).
Derivative of a function f(x) exists for any x R . Let's find her:
= (x 2 – 2x+ 2)′ = 2 x – 2.
Then f(x 1) = x– 2x 1 + 2; (x 1) = 2x 1 – 2. The tangent equation has the form:
y = (2x 1 – 2)(x – x 1) + x– 2x 1 + 2,
y = (2x 1 – 2)x – x+ 2. (1)
Let's find the derivative of the function g(x):
= (–x 2 – 3)′ = –2 x.
Let a function f be given, which at some point x 0 has a finite derivative f (x 0). Then the straight line passing through the point (x 0 ; f (x 0)), having an angular coefficient f ’(x 0), is called a tangent.
What happens if the derivative does not exist at the point x 0? There are two options:
- There is no tangent to the graph either. A classic example is the function y = |x | at point (0; 0).
- The tangent becomes vertical. This is true, for example, for the function y = arcsin x at the point (1; π /2).
Tangent equation
Any non-vertical straight line is given by an equation of the form y = kx + b, where k is the slope. The tangent is no exception, and in order to create its equation at some point x 0, it is enough to know the value of the function and the derivative at this point.
So, let a function y = f (x) be given, which has a derivative y = f ’(x) on the segment. Then at any point x 0 ∈ (a ; b) a tangent can be drawn to the graph of this function, which is given by the equation:
y = f ’(x 0) (x − x 0) + f (x 0)
Here f ’(x 0) is the value of the derivative at point x 0, and f (x 0) is the value of the function itself.
Task. Given the function y = x 3 . Write an equation for the tangent to the graph of this function at the point x 0 = 2.
Tangent equation: y = f ’(x 0) · (x − x 0) + f (x 0). The point x 0 = 2 is given to us, but the values f (x 0) and f ’(x 0) will have to be calculated.
First, let's find the value of the function. Everything is easy here: f (x 0) = f (2) = 2 3 = 8;
Now let’s find the derivative: f ’(x) = (x 3)’ = 3x 2;
We substitute x 0 = 2 into the derivative: f ’(x 0) = f ’(2) = 3 2 2 = 12;
In total we get: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
This is the tangent equation.
Task. Write an equation for the tangent to the graph of the function f (x) = 2sin x + 5 at point x 0 = π /2.
This time we will not describe each action in detail - we will only indicate key steps. We have:
f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f ’(x) = (2sin x + 5)’ = 2cos x;
f ’(x 0) = f ’(π /2) = 2cos (π /2) = 0;
Tangent equation:
y = 0 · (x − π /2) + 7 ⇒ y = 7
IN the latter case the straight line turned out to be horizontal, because its angular coefficient k = 0. There is nothing wrong with this - we just stumbled upon an extremum point.
Consider the following figure:
It depicts a certain function y = f(x), which is differentiable at point a. Point M with coordinates (a; f(a)) is marked. A secant MR is drawn through an arbitrary point P(a + ∆x; f(a + ∆x)) of the graph.
If now point P is shifted along the graph to point M, then straight line MR will rotate around point M. In this case, ∆x will tend to zero. From here we can formulate the definition of a tangent to the graph of a function.
Tangent to the graph of a function
The tangent to the graph of a function is the limiting position of the secant as the increment of the argument tends to zero. It should be understood that the existence of the derivative of the function f at the point x0 means that at this point on the graph there is tangent to him.
In this case, the angular coefficient of the tangent will be equal to the derivative of this function at this point f’(x0). This is the geometric meaning of the derivative. The tangent to the graph of a function f differentiable at point x0 is a certain straight line passing through the point (x0;f(x0)) and having an angular coefficient f’(x0).
Tangent equation
Let's try to obtain the equation of the tangent to the graph of some function f at point A(x0; f(x0)). The equation of a straight line with slope k has the following form:
Since our slope coefficient is equal to the derivative f’(x0), then the equation will take the following form: y = f’(x0)*x + b.
Now let's calculate the value of b. To do this, we use the fact that the function passes through point A.
f(x0) = f’(x0)*x0 + b, from here we express b and get b = f(x0) - f’(x0)*x0.
We substitute the resulting value into the tangent equation:
y = f’(x0)*x + b = f’(x0)*x + f(x0) - f’(x0)*x0 = f(x0) + f’(x0)*(x - x0).
y = f(x0) + f’(x0)*(x - x0).
Let's consider next example: find the equation of the tangent to the graph of the function f(x) = x 3 - 2*x 2 + 1 at point x = 2.
2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.
3. f’(x) = 3*x 2 - 4*x.
4. f’(x0) = f’(2) = 3*2 2 - 4*2 = 4.
5. Substitute the obtained values into the tangent formula, we get: y = 1 + 4*(x - 2). Opening the brackets and bringing similar terms we get: y = 4*x - 7.
Answer: y = 4*x - 7.
General scheme for composing the tangent equation to the graph of the function y = f(x):
1. Determine x0.
2. Calculate f(x0).
3. Calculate f’(x)