Angle between straight lines in space we will call any of the adjacent angles formed by two straight lines drawn through an arbitrary point parallel to the data.
Let two lines be given in space:
Obviously, the angle φ between straight lines can be taken as the angle between their direction vectors and . Since , then using the formula for the cosine of the angle between vectors we get
The conditions of parallelism and perpendicularity of two straight lines are equivalent to the conditions of parallelism and perpendicularity of their direction vectors and:
Two straight parallel if and only if their corresponding coefficients are proportional, i.e. l 1 parallel l 2 if and only if parallel 
.
Two straight perpendicular if and only if the sum of the products of the corresponding coefficients is equal to zero: .
U goal between line and plane
Let it be straight d- not perpendicular to the θ plane;
d′− projection of a line d to the θ plane;
The smallest angle between straight lines d And d′ we will call angle between a straight line and a plane.
Let us denote it as φ=( d,θ)
If d⊥θ, then ( d,θ)=π/2
Oi→j→k→− rectangular coordinate system.
Plane equation:
θ: Ax+By+Cz+D=0
We assume that the straight line is defined by a point and a direction vector: d[M 0,p→]
Vector n→(A,B,C)⊥θ
Then it remains to find out the angle between the vectors n→ and p→, let us denote it as γ=( n→,p→).
If the angle γ<π/2 , то искомый угол φ=π/2−γ .
If the angle is γ>π/2, then the desired angle is φ=γ−π/2
sinφ=sin(2π−γ)=cosγ
sinφ=sin(γ−2π)=−cosγ
Then, angle between straight line and plane can be calculated using the formula:
sinφ=∣cosγ∣=∣ ∣ Ap 1+Bp 2+Cp 3∣ ∣ √A 2+B 2+C 2√p 21+p 22+p 23
Question29. The concept of quadratic form. Sign definiteness of quadratic forms.
Quadratic form j (x 1, x 2, …, x n) n real variables x 1, x 2, …, x n is called a sum of the form 
, (1)
Where a ij – some numbers called coefficients. Without loss of generality, we can assume that a ij = a ji.
The quadratic form is called valid, If a ij
Î GR. Matrix of quadratic form is called a matrix made up of its coefficients. The quadratic form (1) corresponds to the only symmetric matrix 
That is A T = A. Hence, quadratic form(1) can be written in matrix form j ( X) = x T Ah, Where x T = (X 1 X 2 … x n). (2)
And, conversely, every symmetric matrix (2) corresponds to a unique quadratic form up to the notation of variables.
Rank of quadratic form is called the rank of its matrix. The quadratic form is called non-degenerate, if its matrix is non-singular A. (recall that the matrix A is called non-degenerate if its determinant is not equal to zero). Otherwise, the quadratic form is degenerate.
positive definite(or strictly positive) if
j ( X) > 0 , for anyone X = (X 1 , X 2 , …, x n), except X = (0, 0, …, 0).
Matrix A positive definite quadratic form j ( X) is also called positive definite. Therefore, a positive definite quadratic form corresponds to a unique positive definite matrix and vice versa.
The quadratic form (1) is called negatively defined(or strictly negative) if
j ( X) < 0, для любого X = (X 1 , X 2 , …, x n), except X = (0, 0, …, 0).
Similarly as above, a matrix of negative definite quadratic form is also called negative definite.
Consequently, the positive (negative) definite quadratic form j ( X) reaches the minimum (maximum) value j ( X*) = 0 at X* = (0, 0, …, 0).
Note that most quadratic forms are not sign-definite, that is, they are neither positive nor negative. Such quadratic forms vanish not only at the origin of the coordinate system, but also at other points.
When n> 2, special criteria are required to check the sign of a quadratic form. Let's look at them.
Major minors quadratic form are called minors:
that is, these are minors of the order of 1, 2, ..., n matrices A, located in the upper left corner, the last of them coincides with the determinant of the matrix A.
Positive Definiteness Criterion (Sylvester criterion)
X) = x T Ah was positive definite, it is necessary and sufficient that all major minors of the matrix A were positive, that is: M 1 > 0, M 2 > 0, …, Mn > 0. Negative certainty criterion In order for the quadratic form j ( X) = x T Ah was negative definite, it is necessary and sufficient that its principal minors of even order be positive, and of odd order - negative, i.e.: M 1 < 0, M 2 > 0, M 3 < 0, …, (–1)n
With the help of this online calculator you can find the angle between straight lines. Given detailed solution with explanations. To calculate the angle between straight lines, set the dimension (2 if a straight line on a plane is considered, 3 if a straight line in space is considered), enter the elements of the equation into the cells and click on the “Solve” button. See the theoretical part below.
×
Warning
Clear all cells?
Close Clear
Data entry instructions. Numbers are entered as integers (examples: 487, 5, -7623, etc.), decimals (ex. 67., 102.54, etc.) or fractions. The fraction must be entered in the form a/b, where a and b (b>0) are integers or decimals. Examples 45/5, 6.6/76.4, -7/6.7, etc.
1. Angle between straight lines on a plane
Lines are defined by canonical equations
1.1. Determining the angle between straight lines
Let the lines in two-dimensional space L 1 and L
Thus, from formula (1.4) we can find the angle between the straight lines L 1 and L 2. As can be seen from Fig. 1, intersecting lines form adjacent angles φ And φ 1 . If the angle found is greater than 90°, then you can find the minimum angle between straight lines L 1 and L 2: φ 1 =180-φ .
From formula (1.4) we can derive the conditions for parallelism and perpendicularity of two straight lines.
Example 1. Determine the angle between lines
Let's simplify and solve:
1.2. Condition for parallel lines
Let φ =0. Then cosφ=1. In this case, expression (1.4) will take the following form:
| , |
| , |
Example 2. Determine whether the lines are parallel
Equality (1.9) is satisfied, therefore lines (1.10) and (1.11) are parallel.
Answer. Lines (1.10) and (1.11) are parallel.
1.3. Condition for perpendicularity of lines
Let φ =90°. Then cosφ=0. In this case, expression (1.4) will take the following form:
Example 3. Determine whether the lines are perpendicular
Condition (1.13) is satisfied, therefore lines (1.14) and (1.15) are perpendicular.
Answer. Lines (1.14) and (1.15) are perpendicular.
Lines are defined by general equations
1.4. Determining the angle between straight lines
Let two straight lines L 1 and L 2 are given by general equations
From the definition of the scalar product of two vectors, we have:
Example 4. Find the angle between lines
Substituting values A 1 , B 1 , A 2 , B 2 in (1.23), we get:
This angle is greater than 90°. Let's find the minimum angle between straight lines. To do this, subtract this angle from 180:
On the other hand, the condition of parallel lines L 1 and L 2 is equivalent to the condition of collinearity of vectors n 1 and n 2 and can be represented like this:
Equality (1.24) is satisfied, therefore lines (1.26) and (1.27) are parallel.
Answer. Lines (1.26) and (1.27) are parallel.
1.6. Condition for perpendicularity of lines
Condition for perpendicularity of lines L 1 and L 2 can be extracted from formula (1.20) by substituting cos(φ )=0. Then the scalar product ( n 1 ,n 2)=0. Where
Equality (1.28) is satisfied, therefore lines (1.29) and (1.30) are perpendicular.
Answer. Lines (1.29) and (1.30) are perpendicular.
2. Angle between straight lines in space
2.1. Determining the angle between straight lines
Let there be straight lines in space L 1 and L 2 are given by canonical equations
where | q 1 | and | q 2 | direction vector modules q 1 and q 2 respectively, φ -angle between vectors q 1 and q 2 .
From expression (2.3) we obtain:
 .
|
Let's simplify and solve:
 .
|
Let's find the angle φ
Let straight lines be given in space l And m. Through some point A of space we draw straight lines l 1 || l And m 1 || m(Fig. 138).
Note that point A can be chosen arbitrarily; in particular, it can lie on one of these lines. If straight l And m intersect, then A can be taken as the point of intersection of these lines ( l 1 = l And m 1 = m).
Angle between non-parallel lines l And m is the value of the smallest of adjacent angles formed by intersecting lines l 1 And m 1 (l 1 || l, m 1 || m). The angle between parallel lines is considered equal to zero.
Angle between straight lines l And m denoted by \(\widehat((l;m))\). From the definition it follows that if it is measured in degrees, then 0° < \(\widehat((l;m)) \) < 90°, and if in radians, then 0 < \(\widehat((l;m)) \) < π / 2 .
Task. Given a cube ABCDA 1 B 1 C 1 D 1 (Fig. 139).
Find the angle between straight lines AB and DC 1.
Straight lines AB and DC 1 crossing. Since straight line DC is parallel to straight line AB, the angle between straight lines AB and DC 1, according to definition, is equal to \(\widehat(C_(1)DC)\).
Therefore, \(\widehat((AB;DC_1))\) = 45°.
Direct l And m are called perpendicular, if \(\widehat((l;m)) \) = π / 2. For example, in a cube
Calculation of the angle between straight lines.
The problem of calculating the angle between two straight lines in space is solved in the same way as in a plane. Let us denote by φ the magnitude of the angle between the lines l 1 And l 2, and through ψ - the magnitude of the angle between the direction vectors A And b these straight lines.
Then if
ψ <90° (рис. 206, а), то φ = ψ; если же ψ >90° (Fig. 206.6), then φ = 180° - ψ. Obviously, in both cases the equality cos φ = |cos ψ| is true. According to the formula (the cosine of the angle between non-zero vectors a and b is equal to scalar product of these vectors divided by the product of their lengths) we have
$$ cos\psi = cos\widehat((a; b)) = \frac(a\cdot b)(|a|\cdot |b|) $$
hence,
$$ cos\phi = \frac(|a\cdot b|)(|a|\cdot |b|) $$
Let the lines be given by their canonical equations
$$ \frac(x-x_1)(a_1)=\frac(y-y_1)(a_2)=\frac(z-z_1)(a_3) \;\; And \;\; \frac(x-x_2)(b_1)=\frac(y-y_2)(b_2)=\frac(z-z_2)(b_3) $$
Then the angle φ between the lines is determined using the formula
$$ cos\phi = \frac(|a_(1)b_1+a_(2)b_2+a_(3)b_3|)(\sqrt((a_1)^2+(a_2)^2+(a_3)^2 )\sqrt((b_1)^2+(b_2)^2+(b_3)^2)) (1)$$
If one of the lines (or both) is given by non-canonical equations, then to calculate the angle you need to find the coordinates of the direction vectors of these lines, and then use formula (1).
Task 1. Calculate the angle between lines
$$ \frac(x+3)(-\sqrt2)=\frac(y)(\sqrt2)=\frac(z-7)(-2) \;\;and\;\; \frac(x)(\sqrt3)=\frac(y+1)(\sqrt3)=\frac(z-1)(\sqrt6) $$
Direction vectors of straight lines have coordinates:
a = (-√2 ; √2 ; -2), b = (√3 ; √3 ; √6 ).
Using formula (1) we find
$$ cos\phi = \frac(|-\sqrt6+\sqrt6-2\sqrt6|)(\sqrt(2+2+4)\sqrt(3+3+6))=\frac(2\sqrt6)( 2\sqrt2\cdot 2\sqrt3)=\frac(1)(2) $$
Therefore, the angle between these lines is 60°.
Task 2. Calculate the angle between lines
$$ \begin(cases)3x-12z+7=0\\x+y-3z-1=0\end(cases) and \begin(cases)4x-y+z=0\\y+z+1 =0\end(cases) $$
Behind the guide vector A take the first straight line vector product normal vectors n 1 = (3; 0; -12) and n 2 = (1; 1; -3) planes defining this line. Using the formula \(=\begin(vmatrix) i & j & k \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end(vmatrix) \) we get
$$ a==\begin(vmatrix) i & j & k \\ 3 & 0 & -12 \\ 1 & 1 & -3 \end(vmatrix)=12i-3i+3k $$
Similarly, we find the direction vector of the second straight line:
$$ b=\begin(vmatrix) i & j & k \\ 4 & -1 & 1 \\ 0 & 1 & 1 \end(vmatrix)=-2i-4i+4k $$
But using formula (1) we calculate the cosine of the desired angle:
$$ cos\phi = \frac(|12\cdot (-2)-3(-4)+3\cdot 4|)(\sqrt(12^2+3^2+3^2)\sqrt(2 ^2+4^2+4^2))=0 $$
Therefore, the angle between these lines is 90°.
Task 3. IN triangular pyramid MABC edges MA, MB and MS are mutually perpendicular (Fig. 207);
their lengths are respectively 4, 3, 6. Point D is the middle [MA]. Find the angle φ between lines CA and DB.
Let CA and DB be the direction vectors of straight lines CA and DB.
Let's take point M as the origin of coordinates. By the condition of the equation we have A (4; 0; 0), B(0; 0; 3), C(0; 6; 0), D (2; 0; 0). Therefore \(\overrightarrow(CA)\) = (4; - 6;0), \(\overrightarrow(DB)\)= (-2; 0; 3). Let's use formula (1):
$$ cos\phi=\frac(|4\cdot (-2)+(-6)\cdot 0+0\cdot 3|)(\sqrt(16+36+0)\sqrt(4+0+9 )) $$
Using the cosine table, we find that the angle between straight lines CA and DB is approximately 72°.
ANGLE BETWEEN PLANES
Consider two planes α 1 and α 2, defined respectively by the equations:
Under angle between two planes we will understand one of the dihedral angles formed by these planes. It is obvious that the angle between the normal vectors and planes α 1 and α 2 is equal to one of the indicated adjacent dihedral angles or 
. That's why 
. Because 
And 
, That
.
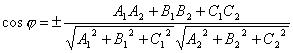Example. Determine the angle between planes x+2y-3z+4=0 and 2 x+3y+z+8=0.
Condition for parallelism of two planes.
Two planes α 1 and α 2 are parallel if and only if their normal vectors are parallel, and therefore 
.
So, two planes are parallel to each other if and only if the coefficients of the corresponding coordinates are proportional:
or
Condition of perpendicularity of planes.
It is clear that two planes are perpendicular if and only if their normal vectors are perpendicular, and therefore, or .
Thus, .
Examples.
STRAIGHT IN SPACE.
VECTOR EQUATION FOR A LINE.
PARAMETRIC DIRECT EQUATIONS
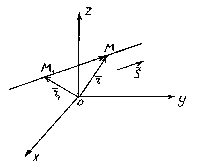
The position of a line in space is completely determined by specifying any of its fixed points M 1 and a vector parallel to this line.
A vector parallel to a line is called guides vector of this line.
So let the straight line l passes through a point M 1 (x 1 , y 1 , z 1), lying on a line parallel to the vector .
Consider an arbitrary point M(x,y,z) on a straight line. From the figure it is clear that 
.
Vectors and are collinear, so there is such a number t, what , where is the multiplier t can take any numeric value depending on the position of the point M on a straight line. Factor t called a parameter. Having designated the radius vectors of points M 1 and M respectively, through and , we obtain . This equation is called vector equation of a straight line. It shows that for each parameter value t corresponds to the radius vector of some point M, lying on a straight line.
Let's write this equation in coordinate form. Notice, that , 
and from here
The resulting equations are called parametric equations of a straight line.
When changing a parameter t coordinates change x, y And z and period M moves in a straight line.
CANONICAL EQUATIONS OF THE DIRECT
Let M 1 (x 1 , y 1 , z 1) – a point lying on a straight line l, And 
is its direction vector. Let us again take an arbitrary point on the line M(x,y,z) and consider the vector .
It is clear that the vectors are also collinear, so their corresponding coordinates must be proportional, therefore,
– canonical equations of a straight line.
Note 1. Note that the canonical equations of the line could be obtained from the parametric ones by eliminating the parameter t. Indeed, from the parametric equations we obtain 
or .
Example. Write down the equation of the line 
in parametric form.
Let's denote 
, from here x = 2 + 3t, y = –1 + 2t, z = 1 –t.
Note 2. Let the straight line be perpendicular to one of the coordinate axes, for example the axis Ox. Then the direction vector of the line is perpendicular Ox, hence, m=0. Consequently, the parametric equations of the line will take the form
Excluding the parameter from the equations t, we obtain the equations of the line in the form
However, in this case too, we agree to formally write the canonical equations of the line in the form 
. Thus, if the denominator of one of the fractions is zero, this means that the straight line is perpendicular to the corresponding coordinate axis.
Similar to the canonical equations 
corresponds to a straight line perpendicular to the axes Ox And Oy or parallel to the axis Oz.
Examples.
GENERAL EQUATIONS OF A STRAIGHT LINE AS LINES OF INTERSECTION OF TWO PLANES
Through every straight line in space there are countless planes. Any two of them, intersecting, define it in space. Consequently, the equations of any two such planes, considered together, represent the equations of this line.
In general, any two non-parallel planes defined by the general equations
determine the straight line of their intersection. These equations are called general equations straight.
Examples.
Construct a line given by the equations 
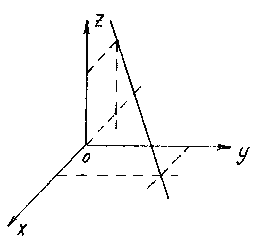
To construct a straight line, it is enough to find any two of its points. The easiest way is to select the points of intersection of the line with coordinate planes. For example, the point of intersection with the plane xOy we obtain from the equations of the straight line, assuming z= 0:
Having solved this system, we find the point M 1 (1;2;0).
Similarly, assuming y= 0, we get the point of intersection of the line with the plane xOz:
From the general equations of a straight line one can move on to its canonical or parametric equations. To do this you need to find some point M 1 on a straight line and the direction vector of a straight line.
Point coordinates M 1 we obtain from this system of equations, giving one of the coordinates an arbitrary value. To find the direction vector, note that this vector must be perpendicular to both normal vectors 
And 
. Therefore, beyond the direction vector of the straight line l you can take the vector product of normal vectors:
.
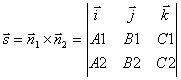Example. Lead general equations straight 
to the canonical form.
Let's find a point lying on a line. To do this, we choose arbitrarily one of the coordinates, for example, y= 0 and solve the system of equations:
The normal vectors of the planes defining the line have coordinates 
Therefore, the direction vector will be straight
. Hence, l: 
.
ANGLE BETWEEN STRAIGHTS
Angle between straight lines in space we will call any of the adjacent angles formed by two straight lines drawn through an arbitrary point parallel to the data.
Let two lines be given in space:
Obviously, the angle φ between straight lines can be taken as the angle between their direction vectors and . Since , then using the formula for the cosine of the angle between vectors we get
This material is devoted to such a concept as the angle between two intersecting lines. In the first paragraph we will explain what it is and show it in illustrations. Then we will look at the ways in which you can find the sine, cosine of this angle and the angle itself (we will separately consider cases with a plane and three-dimensional space), we will give the necessary formulas and show with examples exactly how they are used in practice.
Yandex.RTB R-A-339285-1
In order to understand what the angle formed when two lines intersect is, we need to remember the very definition of angle, perpendicularity and point of intersection.
Definition 1
We call two lines intersecting if they have one common point. This point is called the point of intersection of two lines.
Each straight line is divided by an intersection point into rays. Both straight lines form 4 angles, two of which are vertical, and two are adjacent. If we know the measure of one of them, then we can determine the remaining ones.
Let's say we know that one of the angles is equal to α. In this case, the angle that is vertical with respect to it will also be equal to α. To find the remaining angles, we need to calculate the difference 180 ° - α. If α is equal to 90 degrees, then all angles will be right angles. Lines intersecting at right angles are called perpendicular (a separate article is devoted to the concept of perpendicularity).
Take a look at the picture:
Let's move on to formulating the main definition.
Definition 2
The angle formed by two intersecting lines is the measure of the smaller of the 4 angles that form these two lines.
An important conclusion must be drawn from the definition: the size of the angle in this case will be expressed by any real number in the interval (0, 90]. If the lines are perpendicular, then the angle between them will in any case be equal to 90 degrees.
The ability to find the measure of the angle between two intersecting lines is useful for solving many practical problems. The solution method can be chosen from several options.
To begin with, we can take geometric methods. If we know something about supplementary angles, then we can relate them to the angle we need using the properties of equal or similar figures. For example, if we know the sides of a triangle and need to calculate the angle between the lines on which these sides are located, then the cosine theorem is suitable for solving it. If we have the condition right triangle, then for calculations we will also need knowledge of sine, cosine and tangent of an angle.
The coordinate method is also very convenient for solving problems of this type. Let us explain how to use it correctly.
We have a rectangular (Cartesian) coordinate system O x y, in which two straight lines are given. Let's denote them by letters a and b. The straight lines can be described using some equations. The original lines have an intersection point M. How to determine the required angle (let's denote it α) between these straight lines?
Let's start by formulating the basic principle of finding an angle under given conditions.
We know that the concept of a straight line is closely related to such concepts as a direction vector and a normal vector. If we have an equation of a certain line, we can take the coordinates of these vectors from it. We can do this for two intersecting lines at once.
The angle subtended by two intersecting lines can be found using:
- angle between direction vectors;
- angle between normal vectors;
- the angle between the normal vector of one line and the direction vector of the other.
Now let's look at each method separately.
1. Let us assume that we have a line a with a direction vector a → = (a x, a y) and a line b with a direction vector b → (b x, b y). Now let's plot two vectors a → and b → from the intersection point. After this we will see that they will each be located on their own straight line. Then we have four options for them relative position. See illustration:
If the angle between two vectors is not obtuse, then it will be the angle we need between the intersecting lines a and b. If it is obtuse, then the desired angle will be equal to the angle adjacent to the angle a →, b → ^. Thus, α = a → , b → ^ if a → , b → ^ ≤ 90 ° , and α = 180 ° - a → , b → ^ if a → , b → ^ > 90 ° .
Based on the fact that the cosines equal angles are equal, we can rewrite the resulting equalities as follows: cos α = cos a → , b → ^ , if a → , b → ^ ≤ 90 ° ; cos α = cos 180 ° - a →, b → ^ = - cos a →, b → ^, if a →, b → ^ > 90 °.
In the second case, reduction formulas were used. Thus,
cos α cos a → , b → ^ , cos a → , b → ^ ≥ 0 - cos a → , b → ^ , cos a → , b → ^< 0 ⇔ cos α = cos a → , b → ^
Let's write the last formula in words:
Definition 3
The cosine of the angle formed by two intersecting straight lines will be equal to the modulus of the cosine of the angle between its direction vectors.
The general form of the formula for the cosine of the angle between two vectors a → = (a x , a y) and b → = (b x , b y) looks like this:
cos a → , b → ^ = a → , b → ^ a → b → = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2
From it we can derive the formula for the cosine of the angle between two given straight lines:
cos α = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2 = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2
Then the angle itself can be found using the following formula:
α = a r c cos a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2
Here a → = (a x , a y) and b → = (b x , b y) are the direction vectors of the given lines.
Let's give an example of solving the problem.
Example 1
In a rectangular coordinate system on a plane, two intersecting lines a and b are given. They can be described by the parametric equations x = 1 + 4 · λ y = 2 + λ λ ∈ R and x 5 = y - 6 - 3. Calculate the angle between these lines.
Solution
We have a parametric equation in our condition, which means that for this line we can immediately write down the coordinates of its direction vector. To do this, we need to take the values of the coefficients for the parameter, i.e. the straight line x = 1 + 4 · λ y = 2 + λ λ ∈ R will have a direction vector a → = (4, 1).
The second straight line is described using canonical equation x 5 = y - 6 - 3 . Here we can take the coordinates from the denominators. Thus, this line has a direction vector b → = (5 , - 3) .
Next, we move directly to finding the angle. To do this, simply substitute the existing coordinates of the two vectors into the above formula α = a r c cos a x · b x + a y + b y a x 2 + a y 2 · b x 2 + b y 2 . We get the following:
α = a r c cos 4 5 + 1 (- 3) 4 2 + 1 2 5 2 + (- 3) 2 = a r c cos 17 17 34 = a r c cos 1 2 = 45 °
Answer: These straight lines form an angle of 45 degrees.
We can solve a similar problem by finding the angle between normal vectors. If we have a line a with a normal vector n a → = (n a x , n a y) and a line b with a normal vector n b → = (n b x , n b y), then the angle between them will be equal to the angle between n a → and n b → or the angle that will be adjacent to n a →, n b → ^. This method is shown in the picture:
Formulas for calculating the cosine of the angle between intersecting lines and this angle itself using the coordinates of normal vectors look like this:
cos α = cos n a → , n b → ^ = n a x n b x + n a y + n b y n a x 2 + n a y 2 n b x 2 + n b y 2 α = a r c cos n a x n b x + n a y + n b y n a x 2 + n a y 2 n b x 2 + n b y 2
Here n a → and n b → denote the normal vectors of two given lines.
Example 2
In a rectangular coordinate system, two straight lines are specified using the equations 3 x + 5 y - 30 = 0 and x + 4 y - 17 = 0. Find the sine and cosine of the angle between them and the magnitude of this angle itself.
Solution
The original lines are specified using normal line equations of the form A x + B y + C = 0. We denote the normal vector as n → = (A, B). Let's find the coordinates of the first normal vector for one line and write them: n a → = (3, 5) . For the second line x + 4 y - 17 = 0, the normal vector will have coordinates n b → = (1, 4). Now let’s add the obtained values to the formula and calculate the total:
cos α = cos n a → , n b → ^ = 3 1 + 5 4 3 2 + 5 2 1 2 + 4 2 = 23 34 17 = 23 2 34
If we know the cosine of an angle, then we can calculate its sine using the basic trigonometric identity. Since the angle α formed by straight lines is not obtuse, then sin α = 1 - cos 2 α = 1 - 23 2 34 2 = 7 2 34.
In this case, α = a r c cos 23 2 34 = a r c sin 7 2 34.
Answer: cos α = 23 2 34, sin α = 7 2 34, α = a r c cos 23 2 34 = a r c sin 7 2 34
Let's sort it out last case– finding the angle between straight lines if we know the coordinates of the direction vector of one straight line and the normal vector of the other.
Let us assume that straight line a has a direction vector a → = (a x , a y) , and straight line b has a normal vector n b → = (n b x , n b y) . We need to set these vectors aside from the intersection point and consider all options for their relative positions. See in the picture:
If the angle between given vectors no more than 90 degrees, it turns out that it will complement the angle between a and b to a right angle.
a → , n b → ^ = 90 ° - α if a → , n b → ^ ≤ 90 ° .
If it is less than 90 degrees, then we get the following:
a → , n b → ^ > 90 ° , then a → , n b → ^ = 90 ° + α
Using the rule of equality of cosines of equal angles, we write:
cos a → , n b → ^ = cos (90 ° - α) = sin α for a → , n b → ^ ≤ 90 ° .
cos a → , n b → ^ = cos 90 ° + α = - sin α for a → , n b → ^ > 90 ° .
Thus,
sin α = cos a → , n b → ^ , a → , n b → ^ ≤ 90 ° - cos a → , n b → ^ , a → , n b → ^ > 90 ° ⇔ sin α = cos a → , n b → ^ , a → , n b → ^ > 0 - cos a → , n b → ^ , a → , n b → ^< 0 ⇔ ⇔ sin α = cos a → , n b → ^
Let us formulate a conclusion.
Definition 4
To find the sine of the angle between two lines intersecting on a plane, you need to calculate the modulus of the cosine of the angle between the direction vector of the first line and the normal vector of the second.
Let's write down the necessary formulas. Finding the sine of an angle:
sin α = cos a → , n b → ^ = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2
Finding the angle itself:
α = a r c sin = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2
Here a → is the direction vector of the first line, and n b → is the normal vector of the second.
Example 3
Two intersecting lines are given by the equations x - 5 = y - 6 3 and x + 4 y - 17 = 0. Find the angle of intersection.
Solution
We take the coordinates of the guide and normal vector from the given equations. It turns out a → = (- 5, 3) and n → b = (1, 4). We take the formula α = a r c sin = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2 and calculate:
α = a r c sin = - 5 1 + 3 4 (- 5) 2 + 3 2 1 2 + 4 2 = a r c sin 7 2 34
Please note that we took the equations from the previous problem and obtained exactly the same result, but in a different way.
Answer:α = a r c sin 7 2 34
Let us present another way to find the desired angle using the angular coefficients of given straight lines.
We have a line a, which is defined in a rectangular coordinate system using the equation y = k 1 x + b 1, and a line b, defined as y = k 2 x + b 2. These are equations of straight lines with slopes. To find the angle of intersection, we use the formula:
α = a r c cos k 1 · k 2 + 1 k 1 2 + 1 · k 2 2 + 1, where k 1 and k 2 are angle coefficients given straight lines. To obtain this record, formulas for determining the angle through the coordinates of normal vectors were used.
Example 4
There are two straight lines intersecting in a plane, given by equations y = - 3 5 x + 6 and y = - 1 4 x + 17 4 . Calculate the value of the intersection angle.
Solution
The angular coefficients of our lines are equal to k 1 = - 3 5 and k 2 = - 1 4. Let's add them to the formula α = a r c cos k 1 k 2 + 1 k 1 2 + 1 k 2 2 + 1 and calculate:
α = a r c cos - 3 5 · - 1 4 + 1 - 3 5 2 + 1 · - 1 4 2 + 1 = a r c cos 23 20 34 24 · 17 16 = a r c cos 23 2 34
Answer:α = a r c cos 23 2 34
In the conclusions of this paragraph, it should be noted that the formulas for finding the angle given here do not have to be learned by heart. To do this, it is enough to know the coordinates of the guides and/or normal vectors of given lines and be able to determine them by different types equations. But it’s better to remember or write down the formulas for calculating the cosine of an angle.
How to calculate the angle between intersecting lines in space
The calculation of such an angle can be reduced to calculating the coordinates of the direction vectors and determining the magnitude of the angle formed by these vectors. For such examples, the same reasoning that we gave before is used.
Let's assume that we have a rectangular coordinate system located in three-dimensional space. It contains two straight lines a and b with an intersection point M. To calculate the coordinates of the direction vectors, we need to know the equations of these lines. Let us denote the direction vectors a → = (a x , a y , a z) and b → = (b x , b y , b z) . To calculate the cosine of the angle between them, we use the formula:
cos α = cos a → , b → ^ = a → , b → a → b → = a x b x + a y b y + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2
To find the angle itself, we need this formula:
α = a r c cos a x b x + a y b y + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2
Example 5
We have a line defined in three-dimensional space using the equation x 1 = y - 3 = z + 3 - 2. It is known that it intersects with the O z axis. Calculate the intercept angle and the cosine of that angle.
Solution
Let us denote the angle that needs to be calculated by the letter α. Let's write down the coordinates of the direction vector for the first straight line – a → = (1, - 3, - 2) . For the axis applicate we can take coordinate vector k → = (0, 0, 1) as a guide. We have received the necessary data and can add it to the desired formula:
cos α = cos a → , k → ^ = a → , k → a → k → = 1 0 - 3 0 - 2 1 1 2 + (- 3) 2 + (- 2) 2 0 2 + 0 2 + 1 2 = 2 8 = 1 2
As a result, we found that the angle we need will be equal to a r c cos 1 2 = 45 °.
Answer: cos α = 1 2 , α = 45 ° .
If you notice an error in the text, please highlight it and press Ctrl+Enter