Comment trouver l'angle entre des lignes droites. Angle entre lignes droites en ligne

28.09.2019

Angle entre les lignes droites dans l'espace, nous appellerons n'importe lequel des angles adjacents formés par deux lignes droites passant par un point arbitraire parallèle aux données.

Soit deux droites dans l'espace :

Évidemment, l'angle φ entre les droites peut être considéré comme l'angle entre leurs vecteurs directeurs et . Puisque , alors en utilisant la formule du cosinus de l'angle entre les vecteurs, nous obtenons

Les conditions de parallélisme et de perpendiculaire de deux droites sont équivalentes aux conditions de parallélisme et de perpendiculaire de leurs vecteurs directeurs et :

Deux de suite parallèle si et seulement si leurs coefficients correspondants sont proportionnels, c'est-à-dire je 1 parallèle je 2 si et seulement si parallèle .

Deux de suite perpendiculaire si et seulement si la somme des produits des coefficients correspondants est égale à zéro : .

U but entre la ligne et le plan

Que ce soit direct d- non perpendiculaire au plan θ ;
d′− projection d'une droite d au plan θ ;
Le plus petit angle entre des lignes droites d Et d' nous appellerons angle entre une droite et un plan.
Notons-le par φ=( d,θ)
Si d⊥θ, alors ( d,θ)=π/2

oh→j→k→− système de coordonnées rectangulaires.
Équation plane :

θ: Hache+Par+CZ+D=0

On suppose que la droite est définie par un point et un vecteur directeur : d[M 0,p→]
Vecteur n→(UN,B,C)⊥θ
Reste ensuite à connaître l'angle entre les vecteurs n→ et p→, notons-le γ=( n→,p→).

Si l'angle γ<π/2 , то искомый угол φ=π/2−γ .

Si l'angle est γ>π/2, alors l'angle souhaité est φ=γ−π/2

sinφ=sin(2π−γ)=cosγ

sinφ=sin(γ−2π)=−cosγ

Alors, angle entre la droite et le plan peut être calculé à l'aide de la formule :

sinφ=∣cosγ∣=∣ ∣ Ap 1+Pb 2+CP 3∣ ∣ √UN 2+B 2+C 2√p 21+p 22+p 23

Question29. Le concept de forme quadratique. Signe la définition des formes quadratiques.

Forme quadratique j (x 1, x 2, …, x n) n variables réelles x 1, x 2, …, x n est appelé une somme de la forme
, (1)

Où un ij – quelques nombres appelés coefficients. Sans perte de généralité, on peut supposer que un ij = un ji.

La forme quadratique s'appelle valide, Si un ij Î GR. Matrice de forme quadratique s'appelle une matrice composée de ses coefficients. La forme quadratique (1) correspond à la seule matrice symétrique
C'est UNE T = UNE. Ainsi, forme quadratique(1) peut être écrit en forme matricielle j ( X) = x T Ah, Où xT = (X 1 X 2 … xn). (2)

Et, inversement, toute matrice symétrique (2) correspond à une forme quadratique unique jusqu'à la notation des variables.

Rang de forme quadratique est appelé le rang de sa matrice. La forme quadratique s'appelle non dégénéré, si sa matrice est non singulière UN. (rappelons que la matrice UN est dit non dégénéré si son déterminant n'est pas égal à zéro). Sinon, la forme quadratique est dégénérée.

définie positive(ou strictement positif) si

j ( X) > 0 , pour tout le monde X = (X 1 , X 2 , …, xn), sauf X = (0, 0, …, 0).

Matrice UN forme quadratique définie positive j ( X) est également appelé défini positif. Par conséquent, à une matrice définie positive unique correspond une forme quadratique définie positive et vice versa.

La forme quadratique (1) est appelée défini négativement(ou strictement négatif) si

j ( X) < 0, для любого X = (X 1 , X 2 , …, xn), sauf X = (0, 0, …, 0).

De la même manière que ci-dessus, une matrice de forme quadratique définie négative est également appelée définie négative.

Par conséquent, la forme quadratique définie positive (négative) j ( X) atteint la valeur minimale (maximale) j ( X*) = 0 à X* = (0, 0, …, 0).

Notez que la plupart des formes quadratiques ne sont pas définies par un signe, c'est-à-dire qu'elles ne sont ni positives ni négatives. De telles formes quadratiques disparaissent non seulement à l’origine du système de coordonnées, mais également en d’autres points.

Quand n> 2, des critères particuliers sont nécessaires pour vérifier le signe d'une forme quadratique. Regardons-les.

Mineurs majeurs les formes quadratiques sont appelées mineurs :

c'est-à-dire qu'il s'agit de mineurs de l'ordre de 1, 2, ..., n matrices UN, situé dans le coin supérieur gauche, le dernier d'entre eux coïncide avec le déterminant de la matrice UN.

Critère de certitude positive (Critère Sylvester)

X) = x T Ahétait positif défini, il faut et il suffit que tous les mineurs majeurs de la matrice UNétaient positifs, c'est-à-dire : M 1 > 0, M 2 > 0, …, Mn > 0. Critère de certitude négatif Pour que la forme quadratique j ( X) = x T Ahétait défini négatif, il est nécessaire et suffisant que ses principaux mineurs d'ordre pair soient positifs, et d'ordre impair - négatifs, c'est-à-dire : M 1 < 0, M 2 > 0, M 3 < 0, …, (–1)n

Avec l'aide de ceci calculateur en ligne vous pouvez trouver l'angle entre des lignes droites. Donné solution détaillée avec des explications. Pour calculer l'angle entre des droites, définissez la dimension (2 si l'on considère une droite sur un plan, 3 si l'on considère une droite dans l'espace), entrez les éléments de l'équation dans les cellules et cliquez sur le bouton « Résoudre ». bouton. Voir la partie théorique ci-dessous.

Avertissement

Effacer toutes les cellules ?

Fermer Effacer

Instructions pour la saisie des données. Les nombres sont saisis sous forme de nombres entiers (exemples : 487, 5, -7623, etc.), décimaux (ex. 67., 102,54, etc.) ou de fractions. La fraction doit être saisie sous la forme a/b, où a et b (b>0) sont des nombres entiers ou décimaux. Exemples 45/5, 6,6/76,4, -7/6,7, etc.

1. Angle entre des lignes droites sur un plan

Les lignes sont définies par des équations canoniques

1.1. Déterminer l'angle entre des lignes droites

Laissez les lignes dans l'espace bidimensionnel L 1 et L

Ainsi, à partir de la formule (1.4), nous pouvons trouver l'angle entre les lignes L 1 et L 2. Comme le montre la figure 1, les lignes qui se croisent forment des angles adjacents. φ Et φ 1 . Si l'angle trouvé est supérieur à 90°, alors vous pouvez trouver l'angle minimum entre les droites L 1 et L 2: φ 1 =180-φ .

De la formule (1.4), nous pouvons déduire les conditions de parallélisme et de perpendiculaire de deux droites.

Exemple 1. Déterminer l'angle entre les lignes

Simplifions et résolvons :

1.2. Condition pour les lignes parallèles

Laisser φ =0. Alors cosφ=1. Dans ce cas, l’expression (1.4) prendra la forme suivante :

Exemple 2 : Déterminer si les lignes sont parallèles

L'égalité (1.9) est satisfaite, donc les droites (1.10) et (1.11) sont parallèles.

Répondre. Les droites (1.10) et (1.11) sont parallèles.

1.3. Condition de perpendiculaire des lignes

Laisser φ =90°. Alors cosφ=0. Dans ce cas, l’expression (1.4) prendra la forme suivante :

Exemple 3. Déterminer si les lignes sont perpendiculaires

La condition (1.13) est satisfaite, donc les droites (1.14) et (1.15) sont perpendiculaires.

Répondre. Les droites (1.14) et (1.15) sont perpendiculaires.

Les lignes sont définies par des équations générales

1.4. Déterminer l'angle entre des lignes droites

Soit deux lignes droites L 1 et L 2 sont donnés par des équations générales

De la définition du produit scalaire de deux vecteurs, on a :

Exemple 4. Trouver l'angle entre les lignes

Remplacement des valeurs UN 1 , B 1 , UN 2 , B 2 po (1,23), on obtient :

Cet angle est supérieur à 90°. Trouvons l'angle minimum entre les lignes droites. Pour cela, soustrayez cet angle de 180 :

Par contre, la condition des droites parallèles L 1 et L 2 équivaut à la condition de colinéarité des vecteurs n 1 et n 2 et peut être représenté ainsi :

L'égalité (1.24) est satisfaite, donc les droites (1.26) et (1.27) sont parallèles.

Répondre. Les droites (1.26) et (1.27) sont parallèles.

1.6. Condition de perpendiculaire des lignes

Condition de perpendiculaire des lignes L 1 et L 2 peut être extrait de la formule (1.20) en remplaçant parce que(φ )=0. Alors le produit scalaire ( n 1 ,n 2)=0. Où

L'égalité (1.28) est satisfaite, donc les droites (1.29) et (1.30) sont perpendiculaires.

Répondre. Les droites (1.29) et (1.30) sont perpendiculaires.

2. Angle entre des lignes droites dans l'espace

2.1. Déterminer l'angle entre des lignes droites

Qu'il y ait des lignes droites dans l'espace L 1 et L 2 sont donnés par des équations canoniques

où | q 1 | et | q 2 | modules vectoriels de direction q 1 et q 2 respectivement, φ -angle entre les vecteurs q 1 et q 2 .

De l’expression (2.3) on obtient :

Simplifions et résolvons :

Trouvons l'angle φ

Soit des lignes droites dans l'espace je Et m. Par un point A de l'espace, nous traçons des lignes droites je 1 || je Et m 1 || m(Fig. 138).

A noter que le point A peut être choisi arbitrairement notamment, il peut se situer sur l'une de ces droites ; Si droit je Et m se croisent, alors A peut être pris comme point d'intersection de ces lignes ( je 1 = je Et m 1 = m).

Angle entre des lignes non parallèles je Et m est la valeur du plus petit des angles adjacents formés par des lignes sécantes je 1 Et m 1 (je 1 || je, m 1 || m). L'angle entre les lignes parallèles est considéré comme égal à zéro.

Angle entre les lignes droites je Et m noté $\widehat((l;m))$. De la définition, il s'ensuit que si elle est mesurée en degrés, alors 0° < $\chapeau large((l;m)) $ < 90°, et si en radians, alors 0 < $\chapeau large((l;m)) $ < π / 2 .

Tâche.Étant donné un cube ABCDA 1 B 1 C 1 D 1 (Fig. 139).

Trouvez l'angle entre les droites AB et DC 1.

Traversée des lignes droites AB et DC 1. Puisque la droite DC est parallèle à la droite AB, l'angle entre les droites AB et DC 1, selon la définition, est égal à $\widehat(C_(1)DC)$.

Par conséquent, $\widehat((AB;DC_1))$ = 45°.

Direct je Et m sont appelés perpendiculaire, si $\widehat((l;m)) $ = π / 2. Par exemple, dans un cube

Calcul de l'angle entre droites.

Le problème du calcul de l'angle entre deux droites dans l'espace se résout de la même manière que dans un plan. Notons φ la grandeur de l'angle entre les droites je 1 Et je 2, et via ψ - la grandeur de l'angle entre les vecteurs directeurs UN Et b ces lignes droites.

Puis si

ψ <90° (рис. 206, а), то φ = ψ; если же ψ >90° (Fig. 206.6), alors φ = 180° - ψ. Évidemment, dans les deux cas, l’égalité cos φ = |cos ψ| est vraie. D'après la formule (le cosinus de l'angle entre les vecteurs non nuls a et b est égal à produit scalaire de ces vecteurs divisé par le produit de leurs longueurs) on a

$$ cos\psi = cos\widehat((a; b)) = \frac(a\cdot b)(|a|\cdot |b|) $$

ainsi,

$$ cos\phi = \frac(|a\cdot b|)(|a|\cdot |b|) $$

Soit les droites données par leurs équations canoniques

$$ \frac(x-x_1)(a_1)=\frac(y-y_1)(a_2)=\frac(z-z_1)(a_3) \;\; Et \;\; \frac(x-x_2)(b_1)=\frac(y-y_2)(b_2)=\frac(z-z_2)(b_3) $$

Ensuite, l'angle φ entre les lignes est déterminé à l'aide de la formule

$$ cos\phi = \frac(|a_(1)b_1+a_(2)b_2+a_(3)b_3|)(\sqrt((a_1)^2+(a_2)^2+(a_3)^2 )\sqrt((b_1)^2+(b_2)^2+(b_3)^2)) (1)$$

Si l'une des lignes (ou les deux) est donnée par des équations non canoniques, alors pour calculer l'angle, vous devez trouver les coordonnées des vecteurs directeurs de ces lignes, puis utiliser la formule (1).

Tache 1. Calculer l'angle entre les lignes

$$ \frac(x+3)(-\sqrt2)=\frac(y)(\sqrt2)=\frac(z-7)(-2) \;\;et\;\; \frac(x)(\sqrt3)=\frac(y+1)(\sqrt3)=\frac(z-1)(\sqrt6) $$

Les vecteurs directeurs des droites ont pour coordonnées :

une = (-√2 ; √2 ; -2), b = (√3 ; √3 ; √6 ).

En utilisant la formule (1), nous trouvons

$$ cos\phi = \frac(|-\sqrt6+\sqrt6-2\sqrt6|)(\sqrt(2+2+4)\sqrt(3+3+6))=\frac(2\sqrt6)( 2\sqrt2\cdot 2\sqrt3)=\frac(1)(2) $$

L’angle entre ces lignes est donc de 60°.

Tâche 2. Calculer l'angle entre les lignes

$$ \begin(cases)3x-12z+7=0\\x+y-3z-1=0\end(cases) et \begin(cases)4x-y+z=0\\y+z+1 =0\fin(cas)$$

Derrière le vecteur guide UN prends la première ligne droite produit vectoriel vecteurs normaux n 1 = (3 ; 0 ; -12) et n 2 = (1; 1; -3) plans définissant cette ligne. En utilisant la formule $=\begin(vmatrix) i & j & k \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end(vmatrix) $ nous obtenons

$$ a==\begin(vmatrix) i & j & k \\ 3 & 0 & -12 \\ 1 & 1 & -3 \end(vmatrix)=12i-3i+3k $$

De même, on retrouve le vecteur directeur de la deuxième droite :

$$ b=\begin(vmatrix) i & j & k \\ 4 & -1 & 1 \\ 0 & 1 & 1 \end(vmatrix)=-2i-4i+4k $$

Mais en utilisant la formule (1), nous calculons le cosinus de l'angle souhaité :

$$ cos\phi = \frac(|12\cdot (-2)-3(-4)+3\cdot 4|)(\sqrt(12^2+3^2+3^2)\sqrt(2 ^2+4^2+4^2))=0 $$

L’angle entre ces lignes est donc de 90°.

Tâche 3. DANS pyramide triangulaire Les bords MABC MA, MB et MS sont mutuellement perpendiculaires (Fig. 207) ;

leurs longueurs sont respectivement 4, 3, 6. Le point D est le milieu [MA]. Trouvez l'angle φ entre les lignes CA et DB.

Soit CA et DB les vecteurs directeurs des droites CA et DB.

Prenons le point M comme origine des coordonnées. Par la condition de l'équation, nous avons A (4 ; 0 ; 0), B(0 ; 0 ; 3), C(0 ; 6 ; 0), D (2 ; 0 ; 0). Donc $\overrightarrow(CA)$ = (4; - 6;0), $\overrightarrow(DB)$= (-2; 0; 3). Utilisons la formule (1) :

$$ cos\phi=\frac(|4\cdot (-2)+(-6)\cdot 0+0\cdot 3|)(\sqrt(16+36+0)\sqrt(4+0+9 )) $$

En utilisant la table des cosinus, nous constatons que l’angle entre les droites CA et DB est d’environ 72°.

ANGLE ENTRE PLANS

Considérons deux plans α 1 et α 2, définis respectivement par les équations :

Sous angle entre deux plans on comprendra l'un des angles dièdres formés par ces plans. Il est évident que l'angle entre les vecteurs normaux et les plans α 1 et α 2 est égal à l'un des angles dièdres adjacents indiqués ou . C'est pourquoi . Parce que Et , Que

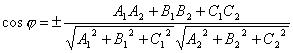Exemple. Déterminer l'angle entre les plans X+2oui-3z+4=0 et 2 X+3oui+z+8=0.

Condition de parallélisme de deux plans.

Deux plans α 1 et α 2 sont parallèles si et seulement si leurs vecteurs normaux sont parallèles, et donc .

Ainsi, deux plans sont parallèles entre eux si et seulement si les coefficients des coordonnées correspondantes sont proportionnels :

Condition de perpendiculaire des plans.

Il est clair que deux plans sont perpendiculaires si et seulement si leurs vecteurs normaux sont perpendiculaires, et donc, ou .

Ainsi, .

Exemples.

DROIT DANS L'ESPACE.

ÉQUATION VECTORIELLE POUR UNE LIGNE.

ÉQUATIONS DIRECTES PARAMÉTRIQUES

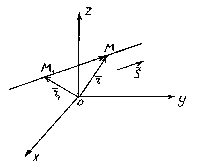
La position d'une ligne dans l'espace est entièrement déterminée en spécifiant l'un de ses points fixes M 1 et un vecteur parallèle à cette droite.

Un vecteur parallèle à une droite s’appelle guides vecteur de cette ligne.

Alors laisse la ligne droite je passe par un point M 1 (X 1 , oui 1 , z 1), situé sur une droite parallèle au vecteur .

Considérons un point arbitraire M(x,y,z) sur une ligne droite. D'après la figure, il ressort clairement que .

Les vecteurs et sont colinéaires, il existe donc un tel nombre t, quoi, où est le multiplicateur t peut prendre n'importe quelle valeur numérique en fonction de la position du point M sur une ligne droite. Facteur t appelé paramètre. Après avoir désigné les rayons vecteurs des points M 1 et M respectivement, grâce à et , on obtient . Cette équation s'appelle vecteuréquation d'une droite. Cela montre que pour chaque valeur de paramètre t correspond au rayon vecteur d'un point M, couché sur une ligne droite.

Écrivons cette équation sous forme de coordonnées. Remarquerez que , et d'ici

Les équations résultantes sont appelées paramétriqueéquations d'une droite.

Lors de la modification d'un paramètre t changement de coordonnées X, oui Et z et période M se déplace en ligne droite.

ÉQUATIONS CANONIQUES DU DIRECT

Laisser M 1 (X 1 , oui 1 , z 1) – un point situé sur une droite je, Et est son vecteur directeur. Prenons à nouveau un point arbitraire sur la droite M(x,y,z) et considérons le vecteur .

Il est clair que les vecteurs sont également colinéaires, leurs coordonnées correspondantes doivent donc être proportionnelles, donc

– canoniqueéquations d'une droite.

Note 1. Notez que les équations canoniques de la droite pourraient être obtenues à partir des équations paramétriques en éliminant le paramètre t. En effet, à partir des équations paramétriques on obtient ou .

Exemple.Écrivez l'équation de la droite sous forme paramétrique.

Notons , d'ici X = 2 + 3t, oui = –1 + 2t, z = 1 –t.

Note 2. Soit la droite perpendiculaire à l'un des axes de coordonnées, par exemple l'axe Bœuf. Alors le vecteur directeur de la droite est perpendiculaire Bœuf, ainsi, m=0. Par conséquent, les équations paramétriques de la droite prendront la forme

Exclure le paramètre des équations t, on obtient les équations de la droite sous la forme

Cependant, dans ce cas aussi, on convient d'écrire formellement les équations canoniques de la droite sous la forme . Ainsi, si le dénominateur d'une des fractions est nul, cela signifie que la droite est perpendiculaire à l'axe de coordonnées correspondant.

Semblable aux équations canoniques correspond à une droite perpendiculaire aux axes Bœuf Et Oy ou parallèle à l'axe Oz.

Exemples.

ÉQUATIONS GÉNÉRALES D'UNE LIGNE DROITE COMME LIGNES D'INTERSECTION DE DEUX PLANS

À travers chaque ligne droite de l’espace se trouvent d’innombrables plans. Deux d'entre eux, se croisant, le définissent dans l'espace. Par conséquent, les équations de deux de ces plans, considérées ensemble, représentent les équations de cette droite.

En général, deux plans non parallèles donnés par les équations générales

déterminer la droite de leur intersection. Ces équations sont appelées équations générales droit.

Exemples.

Construire une droite donnée par les équations

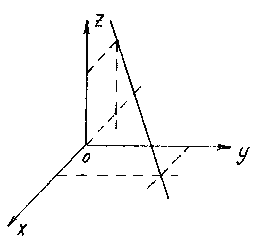
Pour construire une droite, il suffit de trouver deux de ses points. Le plus simple est de sélectionner les points d'intersection de la droite avec plans de coordonnées. Par exemple, le point d'intersection avec le plan xOy on obtient des équations de la droite, en supposant z= 0:

Après avoir résolu ce système, nous trouvons le point M 1 (1;2;0).

De même, en supposant oui= 0, on obtient le point d'intersection de la droite avec le plan xOz:

Des équations générales d'une droite on peut passer à ses équations canoniques ou paramétriques. Pour ce faire, vous devez trouver un point M 1 sur une droite et le vecteur directeur d’une droite.

Coordonnées des points M 1 on obtient de ce système d'équations, donnant à l'une des coordonnées une valeur arbitraire. Pour trouver le vecteur directeur, notez que ce vecteur doit être perpendiculaire aux deux vecteurs normaux Et . Donc, au-delà du vecteur directeur de la droite je vous pouvez prendre le produit vectoriel de vecteurs normaux :

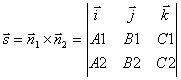Exemple. Plomb équations générales droit à la forme canonique.

Trouvons un point situé sur une ligne. Pour ce faire, on choisit arbitrairement l'une des coordonnées, par exemple, oui= 0 et résolvez le système d'équations :

Les vecteurs normaux des plans définissant la droite ont pour coordonnées Le vecteur direction sera donc droit

. Ainsi, je: .

ANGLE ENTRE DROITES

Angle entre les lignes droites dans l'espace, nous appellerons n'importe lequel des angles adjacents formés par deux lignes droites passant par un point arbitraire parallèle aux données.

Soit deux droites dans l'espace :

Ce document est consacré à un concept tel que l'angle entre deux lignes qui se croisent. Dans le premier paragraphe, nous expliquerons ce que c'est et le montrerons dans des illustrations. Ensuite, nous verrons comment trouver le sinus, le cosinus de cet angle et l'angle lui-même (nous considérerons séparément les cas avec un plan et un espace tridimensionnel), nous donnerons les formules nécessaires et montrerons avec des exemples comment elles sont exactement utilisé dans la pratique.

Yandex.RTB R-A-339285-1

Afin de comprendre quel est l’angle formé lorsque deux lignes se croisent, nous devons nous rappeler la définition même de l’angle, de la perpendiculaire et du point d’intersection.

Définition 1

On appelle deux droites se coupant si elles ont un point commun. Ce point est appelé point d’intersection de deux droites.

Chaque droite est divisée par un point d'intersection en rayons. Les deux lignes droites forment 4 angles, dont deux verticaux et deux adjacents. Si nous connaissons la mesure de l’un d’eux, nous pouvons alors déterminer les autres.

Disons que l'on sait que l'un des angles est égal à α. Dans ce cas, l’angle vertical par rapport à lui sera également égal à α. Pour trouver les angles restants, nous devons calculer la différence 180° - α. Si α est égal à 90 degrés, alors tous les angles seront droits. Les lignes se coupant à angle droit sont appelées perpendiculaires (un article séparé est consacré au concept de perpendiculaire).

Jetez un oeil à la photo :

Passons à la formulation de la définition principale.

Définition 2

L'angle formé par deux lignes sécantes est la mesure du plus petit des 4 angles qui forment ces deux lignes.

Une conclusion importante doit être tirée de la définition : la taille de l'angle dans ce cas sera exprimée par n'importe quel nombre réel dans l'intervalle (0, 90]. Si les lignes sont perpendiculaires, alors l'angle entre elles sera dans tous les cas égal à 90 degrés.

La capacité de trouver la mesure de l’angle entre deux lignes sécantes est utile pour résoudre de nombreux problèmes pratiques. La méthode de résolution peut être choisie parmi plusieurs options.

Pour commencer, nous pouvons prendre des méthodes géométriques. Si nous connaissons quelque chose sur les angles supplémentaires, nous pouvons alors les relier à l’angle dont nous avons besoin en utilisant les propriétés de figures égales ou similaires. Par exemple, si nous connaissons les côtés d'un triangle et devons calculer l'angle entre les lignes sur lesquelles se trouvent ces côtés, alors le théorème du cosinus convient à notre solution. Si nous avons la condition triangle rectangle, alors pour les calculs, nous aurons également besoin de la connaissance du sinus, du cosinus et de la tangente d'un angle.

La méthode des coordonnées est également très pratique pour résoudre des problèmes de ce type. Expliquons comment l'utiliser correctement.

Nous avons un système de coordonnées rectangulaires (cartésiennes) O x y, dans lequel deux lignes droites sont données. Désignons-les par les lettres a et b. Les lignes droites peuvent être décrites à l'aide de certaines équations. Les lignes originales ont un point d'intersection M. Comment déterminer l'angle recherché (notons-le α) entre ces droites ?

Commençons par formuler le principe de base pour trouver un angle dans des conditions données.

Nous savons que le concept de ligne droite est étroitement lié à des concepts tels que vecteur directeur et vecteur normal. Si nous avons une équation d’une certaine droite, nous pouvons en tirer les coordonnées de ces vecteurs. Nous pouvons faire cela pour deux lignes qui se croisent à la fois.

L’angle sous-tendu par deux lignes sécantes peut être trouvé en utilisant :

angle entre les vecteurs directeurs ;
angle entre les vecteurs normaux ;
l'angle entre le vecteur normal d'une ligne et le vecteur directeur de l'autre.

Examinons maintenant chaque méthode séparément.

1. Supposons que nous ayons une droite a avec un vecteur directeur a → = (a x, a y) et une droite b avec un vecteur directeur b → (b x, b y). Traçons maintenant deux vecteurs a → et b → à partir du point d'intersection. Nous verrons ensuite qu'ils seront chacun situés sur leur propre ligne droite. Ensuite, nous avons quatre options pour eux position relative. Voir l'illustration :

Si l’angle entre deux vecteurs n’est pas obtus, alors ce sera l’angle dont nous avons besoin entre les lignes sécantes a et b. S'il est obtus, alors l'angle souhaité sera égal à l'angle adjacent à l'angle a →, b → ^. Ainsi, α = a → , b → ^ si a → , b → ^ ≤ 90 ° , et α = 180 ° - a → , b → ^ si a → , b → ^ > 90 ° .

Basé sur le fait que les cosinus angles égaux sont égaux, on peut réécrire les égalités résultantes comme suit : cos α = cos a → , b → ^ , si a → , b → ^ ≤ 90 ° ; cos α = cos 180° - a →, b → ^ = - cos a →, b → ^, si a →, b → ^ > 90°.

Dans le second cas, des formules de réduction ont été utilisées. Ainsi,

cos α cos a → , b → ^ , cos a → , b → ^ ≥ 0 - cos a → , b → ^ , cos a → , b → ^< 0 ⇔ cos α = cos a → , b → ^

Écrivons la dernière formule avec des mots :

Définition 3

Le cosinus de l'angle formé par deux droites sécantes sera égal au module du cosinus de l'angle entre ses vecteurs directeurs.

La forme générale de la formule du cosinus de l'angle entre deux vecteurs a → = (a x , a y) et b → = (b x , b y) ressemble à ceci :

cos a → , b → ^ = a → , b → ^ a → b → = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2

De là, nous pouvons en déduire la formule du cosinus de l’angle entre deux droites données :

cos α = a x b x + a y + by a x 2 + a y 2 b x 2 + by 2 = a x b x + a y + by a x 2 + a y 2 b x 2 + by 2

Ensuite, l'angle lui-même peut être trouvé à l'aide de la formule suivante :

α = a r c cos a x b x + a y + par a x 2 + a y 2 b x 2 + par y 2

Ici a → = (a x , a y) et b → = (b x , by y) sont les vecteurs directeurs des lignes données.

Donnons un exemple de résolution du problème.

Exemple 1

Dans un système de coordonnées rectangulaires sur un plan, deux lignes sécantes a et b sont données. Ils peuvent être décrits par les équations paramétriques x = 1 + 4 · λ y = 2 + λ λ ∈ R et x 5 = y - 6 - 3. Calculez l'angle entre ces lignes.

Solution

Nous avons une équation paramétrique dans notre condition, ce qui signifie que pour cette droite nous pouvons immédiatement noter les coordonnées de son vecteur directeur. Pour ce faire, il faut prendre les valeurs des coefficients du paramètre, c'est-à-dire la droite x = 1 + 4 λ y = 2 + λ λ ∈ R aura un vecteur directeur a → = (4, 1).

La deuxième ligne droite est décrite par équation canonique x 5 = oui - 6 - 3 . Ici, nous pouvons prendre les coordonnées des dénominateurs. Ainsi, cette droite a un vecteur directeur b → = (5 , - 3) .

Ensuite, nous passons directement à la recherche de l’angle. Pour ce faire, remplacez simplement les coordonnées existantes des deux vecteurs dans la formule ci-dessus α = a r c cos a x · b x + a y + by a x 2 + a y 2 · b x 2 + by y 2 . Nous obtenons ce qui suit :

α = a r c cos 4 5 + 1 (- 3) 4 2 + 1 2 5 2 + (- 3) 2 = a r c cos 17 17 34 = a r c cos 1 2 = 45 °

Répondre: Ces lignes droites forment un angle de 45 degrés.

Nous pouvons résoudre un problème similaire en trouvant l’angle entre les vecteurs normaux. Si nous avons une ligne a avec un vecteur normal n a → = (n a x , n a y) et une ligne b avec un vecteur normal n b → = (n b x , n b y), alors l'angle entre eux sera égal à l'angle entre n a → et n b → ou l'angle qui sera adjacent à n a →, n b → ^. Cette méthode est illustrée dans l'image :

Les formules pour calculer le cosinus de l'angle entre les lignes qui se croisent et cet angle lui-même en utilisant les coordonnées des vecteurs normaux ressemblent à ceci :

cos α = cos n a → , n b → ^ = n a x n b x + n a y + n by n a x 2 + n a y 2 n b x 2 + n by 2 α = a r c cos n a x n b x + n a y + n by n a x 2 + n a y 2 n b x 2 + n by 2

Ici n a → et n b → désignent les vecteurs normaux de deux lignes données.

Exemple 2

Dans un système de coordonnées rectangulaires, deux lignes droites sont spécifiées à l'aide des équations 3 x + 5 y - 30 = 0 et x + 4 y - 17 = 0. Trouvez le sinus et le cosinus de l'angle qui les sépare et la grandeur de cet angle lui-même.

Solution

Les lignes originales sont spécifiées à l'aide d'équations de lignes normales de la forme A x + B y + C = 0. Nous désignons le vecteur normal par n → = (A, B). Trouvons les coordonnées du premier vecteur normal pour une ligne et écrivons-les : n a → = (3, 5) . Pour la deuxième ligne x + 4 y - 17 = 0, le vecteur normal aura les coordonnées n b → = (1, 4). Ajoutons maintenant les valeurs obtenues à la formule et calculons le total :

cos α = cos n a → , n b → ^ = 3 1 + 5 4 3 2 + 5 2 1 2 + 4 2 = 23 34 17 = 23 2 34

Si nous connaissons le cosinus d’un angle, nous pouvons alors calculer son sinus en utilisant l’identité trigonométrique de base. Puisque l'angle α formé par les droites n'est pas obtus, alors sin α = 1 - cos 2 α = 1 - 23 2 34 2 = 7 2 34.

Dans ce cas, α = a r c cos 23 2 34 = a r c sin 7 2 34.

Réponse : cos α = 23 2 34, sin α = 7 2 34, α = a r c cos 23 2 34 = a r c sin 7 2 34

Faisons le tri dernier cas– trouver l'angle entre des droites si l'on connaît les coordonnées du vecteur directeur d'une droite et du vecteur normal de l'autre.

Supposons que la droite a ait un vecteur directeur a → = (a x , a y) et que la droite b ait un vecteur normal n b → = (n b x , n b y) . Nous devons mettre ces vecteurs à l’écart du point d’intersection et considérer toutes les options pour leurs positions relatives. Voir sur la photo :

Si l'angle entre vecteurs donnés pas plus de 90 degrés, il s'avère que cela complétera l'angle entre a et b en un angle droit.

une → , n b → ^ = 90 ° - α si une → , n b → ^ ≤ 90 ° .

S'il fait moins de 90 degrés, alors nous obtenons ce qui suit :

a → , n b → ^ > 90 ° , alors a → , n b → ^ = 90 ° + α

En utilisant la règle d'égalité des cosinus d'angles égaux, on écrit :

cos a → , n b → ^ = cos (90 ° - α) = sin α pour a → , n b → ^ ≤ 90 ° .

cos une → , n b → ^ = cos 90 ° + α = - sin α pour une → , n b → ^ > 90 ° .

Ainsi,

sin α = cos a → , n b → ^ , a → , n b → ^ ≤ 90 ° - cos a → , n b → ^ , a → , n b → ^ > 90 ° ⇔ sin α = cos a → , n b → ^ , une → , n b → ^ > 0 - cos une → , n b → ^ , une → , n b → ^< 0 ⇔ ⇔ sin α = cos a → , n b → ^

Formulons une conclusion.

Définition 4

Pour trouver le sinus de l'angle entre deux droites se coupant sur un plan, vous devez calculer le module du cosinus de l'angle entre le vecteur directeur de la première droite et le vecteur normal de la seconde.

Écrivons les formules nécessaires. Trouver le sinus d'un angle :

sin α = cos a → , n b → ^ = a x n b x + a y n par a x 2 + a y 2 n b x 2 + n par y 2

Trouver l'angle lui-même :

α = a r c sin = a x n b x + a y n par a x 2 + a y 2 n b x 2 + n par y 2

Ici a → est le vecteur directeur de la première ligne, et n b → est le vecteur normal de la seconde.

Exemple 3

Deux droites qui se croisent sont données par les équations x - 5 = y - 6 3 et x + 4 y - 17 = 0. Trouvez l'angle d'intersection.

Solution

Nous prenons les coordonnées du guide et du vecteur normal à partir des équations données. Il s'avère que a → = (- 5, 3) et n → b = (1, 4). Nous prenons la formule α = a r c sin = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2 et calculons :

α = a r c sin = - 5 1 + 3 4 (- 5) 2 + 3 2 1 2 + 4 2 = a r c sin 7 2 34

Veuillez noter que nous avons repris les équations du problème précédent et obtenu exactement le même résultat, mais de manière différente.

Répondre:α = a r c sin 7 2 34

Présentons une autre façon de trouver l'angle souhaité en utilisant les coefficients angulaires de droites données.

Nous avons une ligne a, qui est définie dans un système de coordonnées rectangulaires en utilisant l'équation y = k 1 x + b 1, et une ligne b, définie comme y = k 2 x + b 2. Ce sont des équations de droites avec des pentes. Pour trouver l'angle d'intersection, on utilise la formule :

α = a r c cos k 1 · k 2 + 1 k 1 2 + 1 · k 2 2 + 1, où k 1 et k 2 sont coefficients d'angle donné des lignes droites. Pour obtenir cet enregistrement, des formules permettant de déterminer l'angle grâce aux coordonnées des vecteurs normaux ont été utilisées.

Exemple 4

Il y a deux droites qui se coupent dans un plan, donné par des équations y = - 3 5 x + 6 et y = - 1 4 x + 17 4 . Calculez la valeur de l'angle d'intersection.

Solution

Les coefficients angulaires de nos lignes sont égaux à k 1 = - 3 5 et k 2 = - 1 4. Ajoutons-les à la formule α = a r c cos k 1 k 2 + 1 k 1 2 + 1 k 2 2 + 1 et calculons :

α = a r c cos - 3 5 · - 1 4 + 1 - 3 5 2 + 1 · - 1 4 2 + 1 = a r c cos 23 20 34 24 · 17 16 = a r c cos 23 2 34

Répondre:α = a r c cos 23 2 34

Dans les conclusions de ce paragraphe, il convient de noter que les formules pour trouver l'angle données ici ne doivent pas être apprises par cœur. Pour ce faire, il suffit de connaître les coordonnées des guides et/ou vecteurs normaux de droites données et de pouvoir les déterminer par différents typeséquations. Mais il vaut mieux se souvenir ou noter les formules pour calculer le cosinus d'un angle.

Comment calculer l'angle entre les lignes qui se croisent dans l'espace

Le calcul d'un tel angle peut se réduire au calcul des coordonnées des vecteurs directeurs et à la détermination de l'amplitude de l'angle formé par ces vecteurs. Pour de tels exemples, le même raisonnement que celui que nous avons donné précédemment est utilisé.

Supposons que nous ayons un système de coordonnées rectangulaires situé dans un espace tridimensionnel. Il contient deux droites a et b avec un point d'intersection M. Pour calculer les coordonnées des vecteurs directeurs, il faut connaître les équations de ces droites. Notons les vecteurs directeurs a → = (a x , a y , a z) et b → = (b x , b y , b z) . Pour calculer le cosinus de l'angle qui les sépare, on utilise la formule :

cos α = cos a → , b → ^ = a → , b → a → b → = a x b x + a y b y + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2

Pour trouver l'angle lui-même, nous avons besoin de cette formule :

α = a r c cos a x b x + a y by + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2

Exemple 5

Nous avons une ligne définie dans l'espace tridimensionnel en utilisant l'équation x 1 = y - 3 = z + 3 - 2. On sait qu'il coupe l'axe O z. Calculez l'angle d'origine et le cosinus de cet angle.

Solution

Désignons l'angle qui doit être calculé par la lettre α. Notons les coordonnées du vecteur directeur de la première droite – a → = (1, - 3, - 2) . Pour l'application de l'axe, nous pouvons prendre vecteur de coordonnées k → = (0, 0, 1) à titre indicatif. Nous avons reçu les données nécessaires et pouvons les ajouter à la formule souhaitée :

cos α = cos a → , k → ^ = a → , k → a → k → = 1 0 - 3 0 - 2 1 1 2 + (- 3) 2 + (- 2) 2 0 2 + 0 2 + 1 2 = 2 8 = 1 2

En conséquence, nous avons constaté que l'angle dont nous avons besoin sera égal à a r c cos 1 2 = 45 °.

Répondre: cos α = 1 2 , α = 45 ° .

Si vous remarquez une erreur dans le texte, veuillez la surligner et appuyer sur Ctrl+Entrée