>

Solution de logarithmes fractionnaires. Logarithme népérien, fonction ln x

L'un des éléments de l'algèbre de niveau primitive est le logarithme. Le nom vient de langue grecque du mot « nombre » ou « puissance » et désigne la puissance à laquelle le nombre dans la base doit être élevé pour trouver le nombre final.

Types de logarithmes

  • log a b – logarithme du nombre b en base a (a > 0, a ≠ 1, b > 0) ;
  • log b – logarithme décimal (logarithme en base 10, a = 10) ;
  • ln b – logarithme népérien (logarithme en base e, a = e).

Comment résoudre des logarithmes ?

Le logarithme de b en base a est un exposant qui nécessite que b soit élevé en base a. Le résultat obtenu se prononce ainsi : « logarithme de b en base a ». La solution aux problèmes logarithmiques est que vous devez déterminer la puissance donnée en nombres à partir des nombres spécifiés. Il existe quelques règles de base pour déterminer ou résoudre le logarithme, ainsi que pour convertir la notation elle-même. En les utilisant, la solution est faite équations logarithmiques, les dérivées sont trouvées, les intégrales sont résolues et de nombreuses autres opérations sont effectuées. Fondamentalement, la solution du logarithme lui-même est sa notation simplifiée. Vous trouverez ci-dessous les formules et propriétés de base :

Pour tout un ; une > 0 ; a ≠ 1 et pour tout x ; y > 0.

  • a log a b = b – identité logarithmique de base
  • log a 1 = 0
  • log a = 1
  • log a (x y) = log a x + log a y
  • log a x/ y = log a x – log a y
  • log a 1/x = -log a x
  • log a x p = p log a x
  • log a k x = 1/k log a x , pour k ≠ 0
  • log a x = log a c x c
  • log a x = log b x/ log b a – formule pour passer à une nouvelle base
  • log a x = 1/log x a


Comment résoudre des logarithmes – instructions étape par étape pour la résolution

  • Tout d’abord, notez l’équation requise.

Attention : si le logarithme de base est 10, alors l'entrée est raccourcie, ce qui donne un logarithme décimal. Si ça vaut entier naturel e, puis nous l'écrivons en le réduisant au logarithme népérien. Cela signifie que le résultat de tous les logarithmes est la puissance à laquelle le nombre de base est élevé pour obtenir le nombre b.


Directement, la solution réside dans le calcul de ce degré. Avant de résoudre une expression avec un logarithme, il faut la simplifier selon la règle, c'est-à-dire à l'aide de formules. Vous pourrez retrouver les principales identités en remontant un peu dans l’article.

Additionner et soustraire des logarithmes avec deux différents numéros, mais avec les mêmes bases, remplacez par un logarithme par le produit ou la division des nombres b et c, respectivement. Dans ce cas, vous pouvez appliquer la formule de déplacement vers une autre base (voir ci-dessus).

Si vous utilisez des expressions pour simplifier un logarithme, vous devez prendre en compte certaines limitations. Et c'est : la base du logarithme a n'est qu'un nombre positif, mais pas égal à un. Le nombre b, comme a, doit être supérieur à zéro.

Il existe des cas où, en simplifiant une expression, vous ne pourrez pas calculer numériquement le logarithme. Il arrive qu’une telle expression n’ait aucun sens, car de nombreuses puissances sont des nombres irrationnels. Dans cette condition, laissez la puissance du nombre sous forme de logarithme.



propriétés principales.

  1. logax + logay = loga(x y);
  2. logax − logay = loga (x : y).

motifs identiques

Log6 4 + log6 9.

Maintenant, compliquons un peu la tâche.

Exemples de résolution de logarithmes

Et si la base ou l’argument d’un logarithme était une puissance ? Ensuite, l'exposant de ce degré peut être retiré du signe du logarithme selon les règles suivantes :

Bien entendu, toutes ces règles ont du sens si l'ODZ du logarithme est respectée : a > 0, a ≠ 1, x >

Tâche. Trouvez le sens de l'expression :

Transition vers une nouvelle fondation

Soit le logarithme logax. Alors pour tout nombre c tel que c > 0 et c ≠ 1, l'égalité est vraie :

Tâche. Trouvez le sens de l'expression :

Voir également:


Propriétés de base du logarithme

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.



L'exposant est 2,718281828…. Pour mémoriser l'exposant, vous pouvez étudier la règle : l'exposant est égal à 2,7 et deux fois l'année de naissance de Léon Nikolaïevitch Tolstoï.

Propriétés de base des logarithmes

Connaissant cette règle, vous saurez et valeur exacte exposants, et la date de naissance de Léon Tolstoï.


Exemples de logarithmes

Expressions logarithmiques

Exemple 1.
UN). x=10ac^2 (a>0,c>0).

En utilisant les propriétés 3.5, nous calculons

2.

3.

4. Où .



Exemple 2. Trouver x si


Exemple 3. Soit la valeur des logarithmes

Calculer log(x) si




Propriétés de base des logarithmes

Les logarithmes, comme tous les nombres, peuvent être ajoutés, soustraits et transformés de toutes les manières possibles. Mais comme les logarithmes ne sont pas exactement des nombres ordinaires, il existe ici des règles appelées propriétés principales.

Vous devez absolument connaître ces règles - aucun problème logarithmique sérieux ne peut être résolu sans elles. De plus, il y en a très peu - on peut tout apprendre en une journée. Alors, commençons.

Additionner et soustraire des logarithmes

Considérons deux logarithmes avec les mêmes bases : logax et logay. Ensuite, ils peuvent être ajoutés et soustraits, et :

  1. logax + logay = loga(x y);
  2. logax − logay = loga (x : y).

Ainsi, la somme des logarithmes est égale au logarithme du produit et la différence est égale au logarithme du quotient. Attention : le point clé ici est motifs identiques. Si les raisons sont différentes, ces règles ne fonctionnent pas !

Ces formules vous aideront à calculer expression logarithmique même lorsque ses parties individuelles ne sont pas comptées (voir la leçon « Qu'est-ce qu'un logarithme »). Jetez un œil aux exemples et voyez :

Puisque les logarithmes ont les mêmes bases, nous utilisons la formule de somme :
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Tâche. Trouvez la valeur de l'expression : log2 48 − log2 3.

Les bases sont les mêmes, on utilise la formule de différence :
log2 48 − log2 3 = log2 (48 : 3) = log2 16 = 4.

Tâche. Trouvez la valeur de l'expression : log3 135 − log3 5.

Là encore les bases sont les mêmes, on a donc :
log3 135 − log3 5 = log3 (135 : 5) = log3 27 = 3.

Comme vous pouvez le constater, les expressions originales sont constituées de « mauvais » logarithmes, qui ne sont pas calculés séparément. Mais après les transformations, on obtient des nombres tout à fait normaux. Beaucoup sont construits sur ce fait papiers de test. Oui, des expressions de type test sont proposées très sérieusement (parfois avec pratiquement aucun changement) lors de l'examen d'État unifié.

Extraire l'exposant du logarithme

Il est facile de voir que la dernière règle suit les deux premières. Mais il vaut quand même mieux s'en souvenir - dans certains cas, cela réduira considérablement le nombre de calculs.

Bien sûr, toutes ces règles ont du sens si l'ODZ du logarithme est observé : a > 0, a ≠ 1, x > 0. Et encore une chose : apprenez à appliquer toutes les formules non seulement de gauche à droite, mais aussi vice versa , c'est à dire. Vous pouvez saisir les nombres avant le signe du logarithme dans le logarithme lui-même. C'est ce qui est le plus souvent demandé.

Tâche. Trouvez la valeur de l'expression : log7 496.

Débarrassons-nous du degré dans l'argument en utilisant la première formule :
log7 496 = 6 log7 49 = 6 2 = 12

Tâche. Trouvez le sens de l'expression :

Notez que le dénominateur contient un logarithme dont la base et l'argument sont des puissances exactes : 16 = 24 ; 49 = 72. On a :

Je pense que le dernier exemple nécessite quelques éclaircissements. Où sont passés les logarithmes ? Jusqu'au tout dernier moment nous travaillons uniquement avec le dénominateur.

Formules de logarithme. Exemples de solutions de logarithmes.

Nous avons présenté la base et l'argument du logarithme sous forme de puissances et avons retiré les exposants - nous avons obtenu une fraction « à trois étages ».

Examinons maintenant la fraction principale. Le numérateur et le dénominateur contiennent le même nombre : log2 7. Puisque log2 7 ≠ 0, nous pouvons réduire la fraction - 2/4 resteront au dénominateur. Selon les règles de l'arithmétique, le quatre peut être transféré au numérateur, ce qui a été fait. Le résultat fut la réponse : 2.

Transition vers une nouvelle fondation

En parlant des règles d'addition et de soustraction de logarithmes, j'ai spécifiquement souligné qu'elles ne fonctionnent qu'avec les mêmes bases. Et si les raisons étaient différentes ? Et s’il ne s’agissait pas de puissances exactes du même nombre ?

Les formules de transition vers une nouvelle fondation viennent à la rescousse. Formulons-les sous la forme d'un théorème :

Soit le logarithme logax. Alors pour tout nombre c tel que c > 0 et c ≠ 1, l'égalité est vraie :

En particulier, si on pose c = x, on obtient :

De la deuxième formule, il s'ensuit que la base et l'argument du logarithme peuvent être intervertis, mais dans ce cas, l'expression entière est « retournée », c'est-à-dire le logarithme apparaît au dénominateur.

Ces formules sont rarement trouvées dans les expressions numériques. Il est possible d'évaluer leur commodité uniquement lors de la résolution d'équations logarithmiques et d'inégalités.

Cependant, il existe des problèmes qui ne peuvent être résolus qu’en passant à une nouvelle fondation. Examinons-en quelques-uns :

Tâche. Trouvez la valeur de l'expression : log5 16 log2 25.

Notez que les arguments des deux logarithmes contiennent des puissances exactes. Supprimons les indicateurs : log5 16 = log5 24 = 4log5 2 ; log2 25 = log2 52 = 2log2 5 ;

Maintenant, « inversons » le deuxième logarithme :

Étant donné que le produit ne change pas lors de la réorganisation des facteurs, nous avons calmement multiplié quatre par deux, puis nous sommes occupés des logarithmes.

Tâche. Trouvez la valeur de l'expression : log9 100 lg 3.

La base et l'argument du premier logarithme sont des puissances exactes. Écrivons cela et débarrassons-nous des indicateurs :

Débarrassons-nous maintenant du logarithme décimal en passant à une nouvelle base :

Identité logarithmique de base

Souvent, dans le processus de résolution, il est nécessaire de représenter un nombre sous forme de logarithme sur une base donnée. Dans ce cas, les formules suivantes nous aideront :

Dans le premier cas, le nombre n devient l’exposant de l’argument. Le nombre n peut être absolument n'importe quoi, car il s'agit simplement d'une valeur logarithmique.

La deuxième formule est en fait une définition paraphrasée. C'est comme ça que ça s'appelle : .

En fait, que se passe-t-il si le nombre b est élevé à une puissance telle que le nombre b à cette puissance donne le nombre a ? C'est vrai : le résultat est le même nombre a. Relisez attentivement ce paragraphe – de nombreuses personnes restent bloquées dessus.

Comme les formules pour passer à une nouvelle base, l’identité logarithmique de base est parfois la seule solution possible.

Tâche. Trouvez le sens de l'expression :

Notez que log25 64 = log5 8 - prend simplement le carré de la base et l'argument du logarithme. En tenant compte des règles de multiplication des puissances de même base, on obtient :

Si quelqu'un ne le sait pas, c'était une véritable tâche de l'examen d'État unifié :)

Unité logarithmique et zéro logarithmique

En conclusion, je donnerai deux identités qui peuvent difficilement être qualifiées de propriétés - elles sont plutôt des conséquences de la définition du logarithme. Ils apparaissent constamment dans les problèmes et, étonnamment, créent des problèmes même pour les étudiants « avancés ».

  1. logaa = 1 est. Rappelez-vous une fois pour toutes : le logarithme de n’importe quelle base a de cette base elle-même est égal à un.
  2. loga 1 = 0 est. La base a peut être n'importe quoi, mais si l'argument en contient un, le logarithme est égal à zéro ! Parce que a0 = 1 est une conséquence directe de la définition.

C'est toutes les propriétés. Assurez-vous de vous entraîner à les mettre en pratique ! Téléchargez l'aide-mémoire au début de la leçon, imprimez-la et résolvez les problèmes.

Voir également:

Le logarithme de b en base a désigne l'expression. Calculer le logarithme signifie trouver une puissance x () à laquelle l'égalité est satisfaite

Propriétés de base du logarithme

Il est nécessaire de connaître les propriétés ci-dessus, car presque tous les problèmes et exemples liés aux logarithmes sont résolus sur cette base. Le reste des propriétés exotiques peut être dérivé par des manipulations mathématiques avec ces formules

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

Lorsque vous calculez la formule de la somme et de la différence des logarithmes (3.4), vous la rencontrez assez souvent. Le reste est quelque peu complexe, mais dans un certain nombre de tâches, ils sont indispensables pour simplifier des expressions complexes et calculer leurs valeurs.

Cas courants de logarithmes

Certains des logarithmes les plus courants sont ceux dont la base est égale à dix, exponentielle ou deux.
Le logarithme en base dix est généralement appelé logarithme décimal et est simplement noté lg(x).

Il ressort clairement de l’enregistrement que les bases ne sont pas écrites dans l’enregistrement. Par exemple

Un algorithme naturel est un logarithme avec un exposant comme base (noté ln(x)).

L'exposant est 2,718281828…. Pour mémoriser l'exposant, vous pouvez étudier la règle : l'exposant est égal à 2,7 et deux fois l'année de naissance de Léon Nikolaïevitch Tolstoï. Connaissant cette règle, vous connaîtrez à la fois la valeur exacte de l'exposant et la date de naissance de Léon Tolstoï.

Et un autre logarithme important en base deux est noté

La dérivée du logarithme d'une fonction est égale à un divisé par la variable

Le logarithme intégral ou primitive est déterminé par la relation

Le matériel fourni vous suffit pour résoudre une large classe de problèmes liés aux logarithmes et aux logarithmes. Pour vous aider à comprendre le matériel, je vais donner juste quelques exemples courants de programme scolaire et les universités.

Exemples de logarithmes

Expressions logarithmiques

Exemple 1.
UN). x=10ac^2 (a>0,c>0).

En utilisant les propriétés 3.5, nous calculons

2.
Par la propriété de différence des logarithmes on a

3.
En utilisant les propriétés 3.5, nous trouvons

4. Où .

Une expression apparemment complexe est simplifiée pour être formée à l'aide d'un certain nombre de règles

Trouver des valeurs de logarithme

Exemple 2. Trouver x si

Solution. Pour le calcul, on applique aux derniers termes 5 et 13 les propriétés

Nous l'enregistrons et pleurons

Puisque les bases sont égales, on assimile les expressions

Logarithmes. Premier niveau.

Soit la valeur des logarithmes

Calculer log(x) si

Solution : Prenons un logarithme de la variable pour écrire le logarithme à travers la somme de ses termes


Ce n'est que le début de notre connaissance des logarithmes et de leurs propriétés. Entraînez-vous aux calculs, enrichissez vos compétences pratiques - vous aurez bientôt besoin des connaissances acquises pour résoudre des équations logarithmiques. Après avoir étudié les méthodes de base pour résoudre de telles équations, nous élargirons vos connaissances à un autre sujet tout aussi important : les inégalités logarithmiques...

Propriétés de base des logarithmes

Les logarithmes, comme tous les nombres, peuvent être ajoutés, soustraits et transformés de toutes les manières possibles. Mais comme les logarithmes ne sont pas exactement des nombres ordinaires, il existe ici des règles appelées propriétés principales.

Vous devez absolument connaître ces règles - aucun problème logarithmique sérieux ne peut être résolu sans elles. De plus, il y en a très peu - on peut tout apprendre en une journée. Alors, commençons.

Additionner et soustraire des logarithmes

Considérons deux logarithmes avec les mêmes bases : logax et logay. Ensuite, ils peuvent être ajoutés et soustraits, et :

  1. logax + logay = loga(x y);
  2. logax − logay = loga (x : y).

Ainsi, la somme des logarithmes est égale au logarithme du produit et la différence est égale au logarithme du quotient. Attention : le point clé ici est motifs identiques. Si les raisons sont différentes, ces règles ne fonctionnent pas !

Ces formules vous aideront à calculer une expression logarithmique même lorsque ses parties individuelles ne sont pas prises en compte (voir la leçon « Qu'est-ce qu'un logarithme »). Jetez un œil aux exemples et voyez :

Tâche. Trouvez la valeur de l'expression : log6 4 + log6 9.

Puisque les logarithmes ont les mêmes bases, nous utilisons la formule de somme :
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Tâche. Trouvez la valeur de l'expression : log2 48 − log2 3.

Les bases sont les mêmes, on utilise la formule de différence :
log2 48 − log2 3 = log2 (48 : 3) = log2 16 = 4.

Tâche. Trouvez la valeur de l'expression : log3 135 − log3 5.

Là encore les bases sont les mêmes, on a donc :
log3 135 − log3 5 = log3 (135 : 5) = log3 27 = 3.

Comme vous pouvez le constater, les expressions originales sont constituées de « mauvais » logarithmes, qui ne sont pas calculés séparément. Mais après les transformations, on obtient des nombres tout à fait normaux. De nombreux tests sont basés sur ce fait. Oui, des expressions de type test sont proposées très sérieusement (parfois avec pratiquement aucun changement) lors de l'examen d'État unifié.

Extraire l'exposant du logarithme

Maintenant, compliquons un peu la tâche. Et si la base ou l’argument d’un logarithme était une puissance ? Ensuite, l'exposant de ce degré peut être retiré du signe du logarithme selon les règles suivantes :

Il est facile de voir que la dernière règle suit les deux premières. Mais il vaut quand même mieux s'en souvenir - dans certains cas, cela réduira considérablement le nombre de calculs.

Bien sûr, toutes ces règles ont du sens si l'ODZ du logarithme est observé : a > 0, a ≠ 1, x > 0. Et encore une chose : apprenez à appliquer toutes les formules non seulement de gauche à droite, mais aussi vice versa , c'est à dire. Vous pouvez saisir les nombres avant le signe du logarithme dans le logarithme lui-même.

Comment résoudre des logarithmes

C'est ce qui est le plus souvent demandé.

Tâche. Trouvez la valeur de l'expression : log7 496.

Débarrassons-nous du degré dans l'argument en utilisant la première formule :
log7 496 = 6 log7 49 = 6 2 = 12

Tâche. Trouvez le sens de l'expression :

Notez que le dénominateur contient un logarithme dont la base et l'argument sont des puissances exactes : 16 = 24 ; 49 = 72. On a :

Je pense que le dernier exemple nécessite quelques éclaircissements. Où sont passés les logarithmes ? Jusqu'au tout dernier moment, nous travaillons uniquement avec le dénominateur. Nous avons présenté la base et l'argument du logarithme sous forme de puissances et avons retiré les exposants - nous avons obtenu une fraction « à trois étages ».

Examinons maintenant la fraction principale. Le numérateur et le dénominateur contiennent le même nombre : log2 7. Puisque log2 7 ≠ 0, nous pouvons réduire la fraction - 2/4 resteront au dénominateur. Selon les règles de l'arithmétique, le quatre peut être transféré au numérateur, ce qui a été fait. Le résultat fut la réponse : 2.

Transition vers une nouvelle fondation

En parlant des règles d'addition et de soustraction de logarithmes, j'ai spécifiquement souligné qu'elles ne fonctionnent qu'avec les mêmes bases. Et si les raisons étaient différentes ? Et s’il ne s’agissait pas de puissances exactes du même nombre ?

Les formules de transition vers une nouvelle fondation viennent à la rescousse. Formulons-les sous la forme d'un théorème :

Soit le logarithme logax. Alors pour tout nombre c tel que c > 0 et c ≠ 1, l'égalité est vraie :

En particulier, si on pose c = x, on obtient :

De la deuxième formule, il s'ensuit que la base et l'argument du logarithme peuvent être intervertis, mais dans ce cas, l'expression entière est « retournée », c'est-à-dire le logarithme apparaît au dénominateur.

Ces formules se retrouvent rarement dans les expressions numériques ordinaires. Il est possible d'évaluer leur commodité uniquement lors de la résolution d'équations logarithmiques et d'inégalités.

Cependant, il existe des problèmes qui ne peuvent être résolus qu’en passant à une nouvelle fondation. Examinons-en quelques-uns :

Tâche. Trouvez la valeur de l'expression : log5 16 log2 25.

Notez que les arguments des deux logarithmes contiennent des puissances exactes. Supprimons les indicateurs : log5 16 = log5 24 = 4log5 2 ; log2 25 = log2 52 = 2log2 5 ;

Maintenant, « inversons » le deuxième logarithme :

Étant donné que le produit ne change pas lors de la réorganisation des facteurs, nous avons calmement multiplié quatre par deux, puis nous sommes occupés des logarithmes.

Tâche. Trouvez la valeur de l'expression : log9 100 lg 3.

La base et l'argument du premier logarithme sont des puissances exactes. Écrivons cela et débarrassons-nous des indicateurs :

Débarrassons-nous maintenant du logarithme décimal en passant à une nouvelle base :

Identité logarithmique de base

Souvent, dans le processus de résolution, il est nécessaire de représenter un nombre sous forme de logarithme sur une base donnée. Dans ce cas, les formules suivantes nous aideront :

Dans le premier cas, le nombre n devient l’exposant de l’argument. Le nombre n peut être absolument n'importe quoi, car il s'agit simplement d'une valeur logarithmique.

La deuxième formule est en fait une définition paraphrasée. C'est comme ça que ça s'appelle : .

En fait, que se passe-t-il si le nombre b est élevé à une puissance telle que le nombre b à cette puissance donne le nombre a ? C'est vrai : le résultat est le même nombre a. Relisez attentivement ce paragraphe – de nombreuses personnes restent bloquées dessus.

Comme les formules pour passer à une nouvelle base, l’identité logarithmique de base est parfois la seule solution possible.

Tâche. Trouvez le sens de l'expression :

Notez que log25 64 = log5 8 - prend simplement le carré de la base et l'argument du logarithme. En tenant compte des règles de multiplication des puissances de même base, on obtient :

Si quelqu'un ne le sait pas, c'était une véritable tâche de l'examen d'État unifié :)

Unité logarithmique et zéro logarithmique

En conclusion, je donnerai deux identités qui peuvent difficilement être qualifiées de propriétés - elles sont plutôt des conséquences de la définition du logarithme. Ils apparaissent constamment dans les problèmes et, étonnamment, créent des problèmes même pour les étudiants « avancés ».

  1. logaa = 1 est. Rappelez-vous une fois pour toutes : le logarithme de n’importe quelle base a de cette base elle-même est égal à un.
  2. loga 1 = 0 est. La base a peut être n'importe quoi, mais si l'argument en contient un, le logarithme est égal à zéro ! Parce que a0 = 1 est une conséquence directe de la définition.

C'est toutes les propriétés. Assurez-vous de vous entraîner à les mettre en pratique ! Téléchargez l'aide-mémoire au début de la leçon, imprimez-la et résolvez les problèmes.

Les propriétés de base du logarithme népérien, du graphique, du domaine de définition, de l'ensemble de valeurs, des formules de base, de la dérivée, de l'intégrale, du développement en série de puissance et représentation de la fonction ln x à l'aide de nombres complexes.

Définition

Un algorithme naturel est la fonction y = lnx, l'inverse de l'exponentielle, x = e y, et est le logarithme à la base du nombre e : ln x = log e x.

Le logarithme népérien est largement utilisé en mathématiques car sa dérivée a la forme la plus simple : (lnx)′ = 1/x.

Basé définitions, la base du logarithme népérien est le nombre e:
e ≅ 2,718281828459045...;
.

Graphique de la fonction y = lnx.

Graphique du logarithme népérien (fonctions y = lnx) est obtenu à partir du graphe exponentiel image miroir par rapport à la droite y = x.

Le logarithme népérien est défini pour les valeurs positives de la variable x.

Il augmente de façon monotone dans son domaine de définition. 0 À x →

la limite du logarithme népérien est moins l'infini (-∞). Comme x → + ∞, la limite du logarithme népérien est plus l'infini (+ ∞). Pour x grand, le logarithme augmente assez lentement. N'importe lequel fonction de puissance

x a avec un exposant positif a croît plus vite que le logarithme.

Propriétés du logarithme népérien

Domaine de définition, ensemble de valeurs, extrema, augmentation, diminution

Le logarithme népérien est une fonction croissante de façon monotone, il n’a donc pas d’extrema. Les principales propriétés du logarithme népérien sont présentées dans le tableau.

valeurs ln x

ln 1 = 0

Formules de base pour les logarithmes naturels

Formules issues de la définition de la fonction inverse :

La propriété principale des logarithmes et ses conséquences

Formule de remplacement de base

Tout logarithme peut être exprimé en termes de logarithmes naturels en utilisant la formule de substitution de base :

Des preuves de ces formules sont présentées dans la section "Logarithme".

Fonction inverse

L'inverse du logarithme népérien est l'exposant.

Si donc

Si donc.

Dérivée ln x
.
Dérivée du logarithme népérien :
.
Dérivée du logarithme népérien du module x :
.
Dérivée du nième ordre :

Formules dérivées > > >

Intégral
.
L'intégrale est calculée par intégration par parties :

Donc,

Expressions utilisant des nombres complexes
.
Considérons la fonction de la variable complexe z : Exprimons la variable complexe z par module r φ :
.
et argumentation
.
En utilisant les propriétés du logarithme, on a :
.
Ou
L'argument φ n'est pas défini de manière unique. Si tu mets
, où n est un nombre entier,

ce sera le même numéro pour différents n.

Par conséquent, le logarithme népérien, en fonction d’une variable complexe, n’est pas une fonction à valeur unique.

Extension de la série de puissance

Lorsque l’agrandissement a lieu :
Les références:

DANS. Bronstein, KA (2004). Semendyaev, Manuel de mathématiques pour ingénieurs et étudiants, « Lan », 2009.

\(a^(b)=c\) \(\Leftrightarrow\) \(\log_(a)(c)=b\)

Expliquons-le plus simplement. Par exemple, \(\log_(2)(8)\) est égal à la puissance à laquelle \(2\) doit être élevé pour obtenir \(8\). De là, il est clair que \(\log_(2)(8)=3\).

Exemples:

\(\log_(5)(25)=2\)

parce que \(5^(2)=25\)

\(\log_(3)(81)=4\)

parce que \(3^(4)=81\)

\(\log_(2)\)\(\frac(1)(32)\) \(=-5\)

parce que \(2^(-5)=\)\(\frac(1)(32)\)

Tout logarithme a l’« anatomie » suivante :

L'argument d'un logarithme est généralement écrit à son niveau, et la base est écrite en indice plus proche du signe du logarithme. Et cette entrée se lit comme ceci : « logarithme de vingt-cinq en base cinq ».

Comment calculer le logarithme ?

Pour calculer le logarithme, il faut répondre à la question : à quelle puissance faut-il élever la base pour obtenir l'argument ?

Par exemple, calculez le logarithme : a) \(\log_(4)(16)\) b) \(\log_(3)\)\(\frac(1)(3)\) c) \(\log_(\ sqrt (5))(1)\) d) \(\log_(\sqrt(7))(\sqrt(7))\) e) \(\log_(3)(\sqrt(3))\)

a) À quelle puissance faut-il élever \(4\) pour obtenir \(16\) ? Évidemment le deuxième. C'est pourquoi:

\(\log_(4)(16)=2\)

\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)

c) À quelle puissance faut-il élever \(\sqrt(5)\) pour obtenir \(1\) ? Quel pouvoir fait d’un numéro un ? Zéro, bien sûr !

\(\log_(\sqrt(5))(1)=0\)

d) À quelle puissance faut-il élever \(\sqrt(7)\) pour obtenir \(\sqrt(7)\) ? Premièrement, tout nombre à la puissance première est égal à lui-même.

\(\log_(\sqrt(7))(\sqrt(7))=1\)

e) À quelle puissance faut-il élever \(3\) pour obtenir \(\sqrt(3)\) ? D'après nous, c'est une puissance fractionnaire, ce qui signifie Racine carrée est la puissance de \(\frac(1)(2)\) .

\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)

Exemple : Calculer le logarithme \(\log_(4\sqrt(2))(8)\)

Solution :

\(\log_(4\sqrt(2))(8)=x\)

Nous devons trouver la valeur du logarithme, notons-le x. Utilisons maintenant la définition d'un logarithme :
\(\log_(a)(c)=b\) \(\Leftrightarrow\) \(a^(b)=c\)

\((4\sqrt(2))^(x)=8\)

Qu'est-ce qui relie \(4\sqrt(2)\) et \(8\) ? Deux, car les deux nombres peuvent être représentés par deux :
\(4=2^(2)\) \(\sqrt(2)=2^(\frac(1)(2))\) \(8=2^(3)\)

\(((2^(2)\cdot2^(\frac(1)(2))))^(x)=2^(3)\)

A gauche on utilise les propriétés du degré : \(a^(m)\cdot a^(n)=a^(m+n)\) et \((a^(m))^(n)= a^(m\cdot n)\)

\(2^(\frac(5)(2)x)=2^(3)\)

Les bases sont égales, on passe à l'égalité des indicateurs

\(\frac(5x)(2)\) \(=3\)

Multipliez les deux côtés de l'équation par \(\frac(2)(5)\)

La racine résultante est la valeur du logarithme

Répondre : \(\log_(4\sqrt(2))(8)=1,2\)

Pourquoi le logarithme a-t-il été inventé ?

Pour comprendre cela, résolvons l'équation : \(3^(x)=9\). Faites simplement correspondre \(x\) pour que l'égalité fonctionne. Bien sûr, \(x=2\).

Résolvez maintenant l’équation : \(3^(x)=8\). À quoi x est égal ? C'est le but.

Les plus malins diront : « X vaut un peu moins de deux ». Comment écrire exactement ce numéro ? Pour répondre à cette question, le logarithme a été inventé. Grâce à lui, la réponse ici peut s'écrire \(x=\log_(3)(8)\).

Je tiens à souligner que \(\log_(3)(8)\), comme tout logarithme n'est qu'un nombre. Oui, cela semble inhabituel, mais c'est court. Parce que si nous voulions l'écrire sous forme décimale, cela ressemblerait à ceci : \(1.892789260714.....\)

Exemple : Résolvez l'équation \(4^(5x-4)=10\)

Solution :

\(4^(5x-4)=10\)

\(4^(5x-4)\) et \(10\) ne peuvent pas être amenés à la même base. Cela signifie que vous ne pouvez pas vous passer d’un logarithme.

Utilisons la définition du logarithme :
\(a^(b)=c\) \(\Leftrightarrow\) \(\log_(a)(c)=b\)

\(\log_(4)(10)=5x-4\)

Retournons l'équation pour que X soit à gauche

\(5x-4=\log_(4)(10)\)

Avant nous. Déplaçons \(4\) vers la droite.

Et n’ayez pas peur du logarithme, traitez-le comme un nombre ordinaire.

\(5x=\log_(4)(10)+4\)

Divisez l'équation par 5

\(x=\)\(\frac(\log_(4)(10)+4)(5)\)

C'est notre racine. Oui, cela semble inhabituel, mais ils ne choisissent pas la réponse.

Répondre : \(\frac(\log_(4)(10)+4)(5)\)

Logarithmes décimaux et naturels

Comme indiqué dans la définition d'un logarithme, sa base peut être n'importe quel nombre positif sauf un \((a>0, a\neq1)\). Et parmi toutes les bases possibles, il y en a deux qui apparaissent si souvent qu'une notation courte spéciale a été inventée pour les logarithmes avec elles :

Logarithme naturel : un logarithme dont la base est le nombre d'Euler \(e\) (égal à environ \(2,7182818…\)), et le logarithme s'écrit \(\ln(a)\).

C'est, \(\ln(a)\) est identique à \(\log_(e)(a)\)

Logarithme décimal : Un logarithme dont la base est 10 s'écrit \(\lg(a)\).

C'est, \(\lg(a)\) est identique à \(\log_(10)(a)\), où \(a\) est un nombre.

Identité logarithmique de base

Les logarithmes ont de nombreuses propriétés. L’une d’elles s’appelle « l’identité logarithmique de base » et ressemble à ceci :

\(a^(\log_(a)(c))=c\)

Cette propriété découle directement de la définition. Voyons exactement comment cette formule est née.

Rappelons une courte notation de la définition du logarithme :

si \(a^(b)=c\), alors \(\log_(a)(c)=b\)

Autrement dit, \(b\) est identique à \(\log_(a)(c)\). On peut alors écrire \(\log_(a)(c)\) au lieu de \(b\) dans la formule \(a^(b)=c\). Il s'est avéré que \(a^(\log_(a)(c))=c\) - l'identité logarithmique principale.

Vous pouvez trouver d’autres propriétés des logarithmes. Avec leur aide, vous pouvez simplifier et calculer les valeurs d'expressions avec des logarithmes, difficiles à calculer directement.

Exemple : Trouver la valeur de l'expression \(36^(\log_(6)(5))\)

Solution :

Répondre : \(25\)

Comment écrire un nombre sous forme de logarithme ?

Comme mentionné ci-dessus, tout logarithme n'est qu'un nombre. L’inverse est également vrai : n’importe quel nombre peut être écrit sous forme de logarithme. Par exemple, nous savons que \(\log_(2)(4)\) est égal à deux. Ensuite, vous pouvez écrire \(\log_(2)(4)\) au lieu de deux.

Mais \(\log_(3)(9)\) est également égal à \(2\), ce qui signifie qu'on peut aussi écrire \(2=\log_(3)(9)\) . De même avec \(\log_(5)(25)\), et avec \(\log_(9)(81)\), etc. Autrement dit, il s'avère

\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)

Ainsi, si nous en avons besoin, nous pouvons écrire deux sous forme de logarithme avec n'importe quelle base n'importe où (que ce soit dans une équation, dans une expression ou dans une inégalité) - nous écrivons simplement la base au carré comme argument.

C'est la même chose avec le triple – il peut être écrit sous la forme \(\log_(2)(8)\), ou sous la forme \(\log_(3)(27)\), ou sous la forme \(\log_(4)( 64) \)... Ici, nous écrivons la base dans le cube comme argument :

\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)

Et avec quatre :

\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)

Et avec moins un :

\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1 )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1)(7)\) \(...\)

Et avec un tiers :

\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)

Tout nombre \(a\) peut être représenté sous forme de logarithme de base \(b\) : \(a=\log_(b)(b^(a))\)

Exemple : Trouver le sens de l'expression \(\frac(\log_(2)(14))(1+\log_(2)(7))\)

Solution :

Répondre : \(1\)

Définition du logarithme

Le logarithme de b en base a est l'exposant auquel a doit être élevé pour obtenir b.

Numéro e en mathématiques, il est d'usage de désigner la limite à laquelle une expression s'efforce

Numéro e est nombre irrationnel- un nombre incommensurable avec un, il ne peut être exprimé avec précision ni sous forme d'entier ni de fraction rationnel nombre.

Lettre e- première lettre d'un mot latin exposer- se montrer, d'où le nom en mathématiques exponentiel- fonction exponentielle.

Nombre e largement utilisé en mathématiques et dans toutes les sciences qui, d'une manière ou d'une autre, utilisent les calculs mathématiques pour leurs besoins.

Logarithmes. Propriétés des logarithmes

Définition : Le logarithme d'un nombre positif b à sa base est l'exposant c auquel il faut élever le nombre a pour obtenir le nombre b.

Identité logarithmique de base :

7) Formule de déménagement vers une nouvelle base :

lna = log e a, e ≈ 2,718…

Problèmes et tests sur le thème « Logarithmes. Propriétés des logarithmes"

  • Logarithmes - Sujets importants pour la révision de l'examen d'État unifié en mathématiques

Pour réussir les tâches sur ce sujet, vous devez connaître la définition d'un logarithme, les propriétés des logarithmes, l'identité logarithmique de base, les définitions des logarithmes décimaux et naturels. Les principaux types de problèmes sur ce sujet sont des problèmes impliquant le calcul et la transformation d'expressions logarithmiques. Considérons leur solution à l'aide des exemples suivants.

Solution: En utilisant les propriétés des logarithmes, on obtient

Solution: En utilisant les propriétés des degrés, on obtient

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Propriétés des logarithmes, formulations et preuves.

Les logarithmes ont un certain nombre de propriétés caractéristiques. Dans cet article, nous examinerons les principaux propriétés des logarithmes. Ici, nous donnerons leurs formulations, noterons les propriétés des logarithmes sous forme de formules, montrerons des exemples de leur application et fournirons également la preuve des propriétés des logarithmes.

Navigation dans les pages.

Propriétés de base des logarithmes, formules

Pour faciliter la mémorisation et l'utilisation, imaginons propriétés de base des logarithmes sous la forme d'une liste de formules. Dans le paragraphe suivant, nous donnerons leurs formulations, leurs preuves, leurs exemples d'utilisation et les explications nécessaires.

  • Propriété du logarithme de l'unité : log a 1=0 pour tout a>0, a≠1.
  • Logarithme d'un nombre égal à la base : log a a=1 pour a>0, a≠1.
  • Propriété du logarithme de la puissance de la base : log a a p =p, où a>0, a≠1 et p est un nombre réel quelconque.
  • Logarithme du produit de deux nombres positifs : log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
    et la propriété du logarithme du produit de n nombres positifs : log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x2 >0, …, xn >0 .
  • Propriété du logarithme d'un quotient : , où a>0, a≠1, x>0, y>0.
  • Logarithme de la puissance d'un nombre : log a b p =p·log a |b| , où a>0, a≠1, b et p sont des nombres tels que le degré b p a du sens et b p >0.
  • Conséquence: , où a>0, a≠1, n est un nombre naturel supérieur à un, b>0.
  • Corollaire 1 : , une>0 , une≠1 , b>0 , b≠1 .
  • Corollaire 2 : , a>0 , a≠1 , b>0 , p et q sont des nombres réels, q≠0 , en particulier pour b=a on a .

    • Formulations et preuves de propriétés

    Nous procédons à la formulation et à la preuve des propriétés écrites des logarithmes. Toutes les propriétés des logarithmes sont prouvées sur la base de la définition du logarithme et de l'identité logarithmique de base qui en découle, ainsi que des propriétés du degré.

    Commençons avec propriétés du logarithme de un. Sa formulation est la suivante : le logarithme de l'unité est égal à zéro, c'est-à-dire enregistrer un 1=0 pour tout a>0, a≠1. La preuve n'est pas difficile : puisque a 0 =1 pour tout a satisfaisant les conditions ci-dessus a>0 et a≠1, alors l'égalité log a 1=0 à prouver découle immédiatement de la définition du logarithme.

    Donnons des exemples d'application de la propriété considérée : log 3 1=0, log1=0 et .

    Passons à la propriété suivante : le logarithme d'un nombre égal à la base est égal à un, c'est, log a a = 1 pour une>0, une≠1. En effet, puisque a 1 =a pour tout a, alors par définition du logarithme log a a=1.

    Des exemples d'utilisation de cette propriété des logarithmes sont les égalités log 5 5=1, log 5,6 5,6 et lne=1.

    Le logarithme d'une puissance d'un nombre égal à la base du logarithme est égal à l'exposant. Cette propriété du logarithme correspond à une formule de la forme log a a p =p, où a>0, a≠1 et p – n’importe quel nombre réel. Cette propriété découle directement de la définition du logarithme. A noter qu'il permet d'indiquer immédiatement la valeur du logarithme, s'il est possible de représenter le nombre sous le signe du logarithme comme une puissance de la base ; nous en reparlerons davantage dans l'article calcul des logarithmes.

    Par exemple, log 2 2 7 =7, log10 -4 =-4 et .

    Logarithme du produit de deux nombres positifs x et y sont égaux au produit des logarithmes de ces nombres : log a (x y)=log a x+log a y, une>0 , une≠1 . Démontrons la propriété du logarithme d'un produit. En raison des propriétés du degré a log a x+log a y =a log a x ·a log a y, et puisque par l'identité logarithmique principale a log a x =x et un log a y =y, alors un log a x ·a log a y =x·y. Ainsi, un log a x+log a y =x·y, d'où, par la définition d'un logarithme, découle l'égalité prouvée.

    Montrons des exemples d'utilisation de la propriété du logarithme d'un produit : log 5 (2 3)=log 5 2+log 5 3 et .

    La propriété du logarithme d'un produit peut être généralisée au produit d'un nombre fini n de nombres positifs x 1 , x 2 , …, x n comme log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n. Cette égalité peut être prouvée sans problème en utilisant la méthode d’induction mathématique.

    Par exemple, le logarithme naturel du produit peut être remplacé par la somme de trois logarithmes naturels des nombres 4, e et.

    Logarithme du quotient de deux nombres positifs x et y sont égaux à la différence entre les logarithmes de ces nombres. La propriété du logarithme d'un quotient correspond à une formule de la forme , où a>0, a≠1, x et y sont des nombres positifs. La validité de cette formule est prouvée ainsi que celle du logarithme d'un produit : puisque , alors par définition du logarithme .

    Voici un exemple d'utilisation de cette propriété du logarithme : .

    Passons à propriété du logarithme de la puissance. Le logarithme d'un degré est égal au produit de l'exposant et du logarithme du module de la base de ce degré. Écrivons cette propriété du logarithme d'une puissance sous forme de formule : log a b p =p·log a |b|, où a>0, a≠1, b et p sont des nombres tels que le degré b p a du sens et b p >0.

    Nous prouvons d’abord cette propriété pour b positif. L'identité logarithmique de base nous permet de représenter le nombre b comme un log a b , alors b p =(a log a b) p , et l'expression résultante, en raison de la propriété de puissance, est égale à a p·log a b . On arrive donc à l'égalité b p =a p·log a b, d'où, par la définition d'un logarithme, on conclut que log a b p =p·log a b.

    Il reste à prouver cette propriété pour b négatif. Notons ici que l'expression log a b p pour b négatif n'a de sens que pour les exposants pairs p (puisque la valeur du degré b p doit être supérieure à zéro, sinon le logarithme n'aura pas de sens), et dans ce cas b p =|b| p. Alors bp =|b| p =(a log a |b|) p =a p·log a |b| , d'où log a b p =p·log a |b| .

    Par exemple, et ln(-3) 4 =4·ln|-3|=4·ln3 .

    Il découle de la propriété précédente propriété du logarithme à partir de la racine: le logarithme de la nième racine est égal au produit de la fraction 1/n par le logarithme de l'expression radicale, c'est-à-dire où a>0, a≠1, n est un nombre naturel supérieur à un, b>0 .

    La preuve est basée sur l'égalité (voir définition de l'exposant avec un exposant fractionnaire), qui est valable pour tout b positif, et la propriété du logarithme de l'exposant : .

    Voici un exemple d'utilisation de cette propriété : .

    Maintenant, prouvons formule pour passer à une nouvelle base de logarithme gentil . Pour ce faire, il suffit de prouver la validité de l'égalité log c b=log a b·log c a. L'identité logarithmique de base nous permet de représenter le nombre b comme un log a b , alors log c b=log c a log a b . Il reste à utiliser la propriété du logarithme du degré : log c a log a b =log a b·log c a . Cela prouve l'égalité log c b=log a b·log c a, ce qui signifie que la formule de transition vers une nouvelle base du logarithme est également prouvée .

    Montrons quelques exemples d'utilisation de cette propriété des logarithmes : et .

    La formule de passage à une nouvelle base vous permet de passer au travail avec des logarithmes ayant une base « pratique ». Par exemple, il peut être utilisé pour passer aux logarithmes naturels ou décimaux afin de pouvoir calculer la valeur d'un logarithme à partir d'un tableau de logarithmes. La formule de passage à une nouvelle base de logarithme permet également, dans certains cas, de retrouver la valeur d'un logarithme donné lorsque les valeurs de certains logarithmes avec d'autres bases sont connues.

    Un cas particulier de formule de transition vers une nouvelle base de logarithme pour c=b de la forme est souvent utilisé. Cela montre que log a b et log b a sont des nombres mutuellement inverses. Par exemple, .

    La formule est également souvent utilisée, ce qui est pratique pour trouver les valeurs des logarithmes. Pour confirmer nos propos, nous montrerons comment il peut être utilisé pour calculer la valeur d'un logarithme de la forme . Nous avons . Pour prouver la formule, il suffit d'utiliser la formule de passage à une nouvelle base du logarithme a : .

    Reste à prouver les propriétés de comparaison des logarithmes.

    Utilisons la méthode inverse. Supposons que pour a 1 >1, a 2 >1 et a 1 2 et pour 0 1, log a 1 b≤log a 2 b est vrai. Sur la base des propriétés des logarithmes, ces inégalités peuvent être réécrites comme Et respectivement, et il en résulte que log b a 1 ≤log b a 2 et log b a 1 ≥log b a 2, respectivement. Alors, selon les propriétés des puissances de mêmes bases, les égalités b log b a 1 ≥b log b a 2 et b log b a 1 ≥b log b a 2 doivent être vraies, c'est-à-dire a 1 ≥a 2 . Nous sommes donc arrivés à une contradiction avec la condition a 1 2. Ceci termine la preuve.

    Propriétés de base des logarithmes

    • Matériel pour la leçon
    • Téléchargez toutes les formules

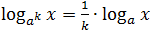
      • Les logarithmes, comme tous les nombres, peuvent être ajoutés, soustraits et transformés de toutes les manières possibles. Mais comme les logarithmes ne sont pas exactement des nombres ordinaires, il existe ici des règles appelées propriétés principales.

      Vous devez absolument connaître ces règles - sans elles, aucun problème logarithmique sérieux ne peut être résolu. De plus, il y en a très peu - on peut tout apprendre en une journée. Alors, commençons.

      Additionner et soustraire des logarithmes

      Considérons deux logarithmes avec les mêmes bases : log a x et log a y. Ensuite, ils peuvent être ajoutés et soustraits, et :

      Ainsi, la somme des logarithmes est égale au logarithme du produit et la différence est égale au logarithme du quotient. Attention : le point clé ici est motifs identiques. Si les raisons sont différentes, ces règles ne fonctionnent pas !

      Ces formules vous aideront à calculer une expression logarithmique même lorsque ses parties individuelles ne sont pas prises en compte (voir la leçon « Qu'est-ce qu'un logarithme »). Jetez un œil aux exemples et voyez :

      Tâche. Trouvez la valeur de l'expression : log 6 4 + log 6 9.

      Puisque les logarithmes ont les mêmes bases, nous utilisons la formule de somme :
      log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

      Tâche. Trouvez la valeur de l'expression : log 2 48 − log 2 3.

      Les bases sont les mêmes, on utilise la formule de différence :
      log 2 48 − log 2 3 = log 2 (48 : 3) = log 2 16 = 4.

      Tâche. Trouvez la valeur de l'expression : log 3 135 − log 3 5.

      Là encore les bases sont les mêmes, on a donc :
      log 3 135 − log 3 5 = log 3 (135 : 5) = log 3 27 = 3.

      Comme vous pouvez le constater, les expressions originales sont constituées de « mauvais » logarithmes, qui ne sont pas calculés séparément. Mais après les transformations, on obtient des nombres tout à fait normaux. De nombreux tests sont basés sur ce fait. Oui, des expressions de type test sont proposées très sérieusement (parfois avec pratiquement aucun changement) lors de l'examen d'État unifié.

      Extraire l'exposant du logarithme

      Maintenant, compliquons un peu la tâche. Et si la base ou l’argument d’un logarithme était une puissance ? Ensuite, l'exposant de ce degré peut être retiré du signe du logarithme selon les règles suivantes :

    • log a x n = n · log a x ;

      • Il est facile de voir que la dernière règle suit les deux premières. Mais il vaut quand même mieux s'en souvenir - dans certains cas, cela réduira considérablement le nombre de calculs.

      Bien sûr, toutes ces règles ont du sens si l'ODZ du logarithme est observé : a > 0, a ≠ 1, x > 0. Et encore une chose : apprenez à appliquer toutes les formules non seulement de gauche à droite, mais aussi vice versa , c'est à dire. Vous pouvez saisir les nombres avant le signe du logarithme dans le logarithme lui-même. C'est ce qui est le plus souvent demandé.

      Tâche. Trouvez la valeur de l'expression : log 7 49 6 .

      Débarrassons-nous du degré dans l'argument en utilisant la première formule :
      log 7 49 6 = 6 log 7 49 = 6 2 = 12

      Tâche. Trouvez le sens de l'expression :

      [Légende de la photo]

      Notez que le dénominateur contient un logarithme dont la base et l'argument sont des puissances exactes : 16 = 2 4 ; 49 = 7 2. Nous avons:

      [Légende de la photo]

      Je pense que le dernier exemple nécessite quelques éclaircissements. Où sont passés les logarithmes ? Jusqu'au tout dernier moment, nous travaillons uniquement avec le dénominateur. Nous avons présenté la base et l'argument du logarithme sous forme de puissances et avons retiré les exposants - nous avons obtenu une fraction « à trois étages ».

      Examinons maintenant la fraction principale. Le numérateur et le dénominateur contiennent le même nombre : log 2 7. Puisque log 2 7 ≠ 0, on peut réduire la fraction - 2/4 resteront au dénominateur. Selon les règles de l'arithmétique, le quatre peut être transféré au numérateur, ce qui a été fait. Le résultat fut la réponse : 2.

      Transition vers une nouvelle fondation

      En parlant des règles d'addition et de soustraction de logarithmes, j'ai spécifiquement souligné qu'elles ne fonctionnent qu'avec les mêmes bases. Et si les raisons étaient différentes ? Et s’il ne s’agissait pas de puissances exactes du même nombre ?

      Les formules de transition vers une nouvelle fondation viennent à la rescousse. Formulons-les sous la forme d'un théorème :

      Soit le logarithme log a x. Alors pour tout nombre c tel que c > 0 et c ≠ 1, l'égalité est vraie :

      [Légende de la photo]

      En particulier, si on pose c = x, on obtient :

      [Légende de la photo]

      De la deuxième formule, il s'ensuit que la base et l'argument du logarithme peuvent être intervertis, mais dans ce cas, l'expression entière est « retournée », c'est-à-dire le logarithme apparaît au dénominateur.

      Ces formules se retrouvent rarement dans les expressions numériques ordinaires. Il est possible d'évaluer leur commodité uniquement lors de la résolution d'équations logarithmiques et d'inégalités.

      Cependant, il existe des problèmes qui ne peuvent être résolus qu’en passant à une nouvelle fondation. Examinons-en quelques-uns :

      Tâche. Trouvez la valeur de l'expression : log 5 16 log 2 25.

      Notez que les arguments des deux logarithmes contiennent des puissances exactes. Sortons les indicateurs : log 5 16 = log 5 2 4 = 4log 5 2 ; journal 2 25 = journal 2 5 2 = 2 journal 2 5 ;

      Maintenant, « inversons » le deuxième logarithme :

      [Légende de la photo]

      Étant donné que le produit ne change pas lors de la réorganisation des facteurs, nous avons calmement multiplié quatre par deux, puis nous sommes occupés des logarithmes.

      Tâche. Trouvez la valeur de l'expression : log 9 100 lg 3.

      La base et l'argument du premier logarithme sont des puissances exactes. Écrivons cela et débarrassons-nous des indicateurs :

      [Légende de la photo]

      Débarrassons-nous maintenant du logarithme décimal en passant à une nouvelle base :

      [Légende de la photo]

      Identité logarithmique de base

      Souvent, dans le processus de résolution, il est nécessaire de représenter un nombre sous forme de logarithme sur une base donnée. Dans ce cas, les formules suivantes nous aideront :

    1. n = journal a a n

    2. Dans le premier cas, le nombre n devient l’exposant de l’argument. Le nombre n peut être absolument n'importe quoi, car il s'agit simplement d'une valeur logarithmique.

      La deuxième formule est en fait une définition paraphrasée. C’est comme ça qu’on l’appelle : l’identité logarithmique de base.

      En fait, que se passe-t-il si le nombre b est élevé à une puissance telle que le nombre b à cette puissance donne le nombre a ? C'est vrai : le résultat est le même nombre a. Relisez attentivement ce paragraphe – de nombreuses personnes restent bloquées dessus.

      Comme les formules pour passer à une nouvelle base, l’identité logarithmique de base est parfois la seule solution possible.

      [Légende de la photo]

      Notez que log 25 64 = log 5 8 - nous avons simplement pris le carré de la base et de l'argument du logarithme. En tenant compte des règles de multiplication des puissances de même base, on obtient :

      [Légende de la photo]

      Si quelqu'un ne le sait pas, c'était une véritable tâche de l'examen d'État unifié :)

      Unité logarithmique et zéro logarithmique

      En conclusion, je donnerai deux identités qui peuvent difficilement être qualifiées de propriétés - elles sont plutôt des conséquences de la définition du logarithme. Ils apparaissent constamment dans les problèmes et, étonnamment, créent des problèmes même pour les étudiants « avancés ».

      1. log a a = 1 est une unité logarithmique. Rappelez-vous une fois pour toutes : le logarithme de n’importe quelle base a de cette base elle-même est égal à un.
      2. log a 1 = 0 est un zéro logarithmique. La base a peut être n'importe quoi, mais si l'argument en contient un, le logarithme est égal à zéro ! Parce que 0 = 1 est une conséquence directe de la définition.

      C'est toutes les propriétés. Assurez-vous de vous entraîner à les mettre en pratique ! Téléchargez l'aide-mémoire au début de la leçon, imprimez-la et résolvez les problèmes.

      Logarithme. Propriétés du logarithme (addition et soustraction).

      Propriétés du logarithme découlent de sa définition. Et donc le logarithme du nombre b basé sur UN est défini comme l'exposant auquel un nombre doit être élevé un pour obtenir le numéro b(le logarithme n'existe que pour les nombres positifs).

      De cette formulation il résulte que le calcul x = journal a b, équivaut à résoudre l’équation un x = b. Par exemple, journal 2 8 = 3 parce que 8 = 2 3 . La formulation du logarithme permet de justifier que si b = un c, puis le logarithme du nombre b basé sur unéquivaut à Avec. Il est également clair que le thème des logarithmes est étroitement lié au thème des puissances.

      Avec les logarithmes, comme avec tous les nombres, vous pouvez faire opérations d'addition, de soustraction et transformer de toutes les manières possibles. Mais étant donné que les logarithmes ne sont pas des nombres entièrement ordinaires, leurs propres règles spéciales s'appliquent ici, appelées propriétés principales.

      Additionner et soustraire des logarithmes.

      Prenons deux logarithmes de mêmes bases : enregistrer un x Et Connectez-vous un y. Il est alors possible d'effectuer des opérations d'addition et de soustraction :

      Comme nous le voyons, somme de logarithmes est égal au logarithme du produit, et différence logarithmes- logarithme du quotient. De plus, cela est vrai si les chiffres UN, X Et à positif et une ≠ 1.

      Il est important de noter que l’aspect principal de ces formules réside dans les mêmes bases. Si les motifs sont différents, ces règles ne s’appliquent pas !

      Les règles d'addition et de soustraction de logarithmes avec les mêmes bases se lisent non seulement de gauche à droite, mais aussi vice versa. En conséquence, nous avons les théorèmes du logarithme du produit et du logarithme du quotient.

      Logarithme du produit deux nombres positifs égal à la somme leurs logarithmes ; en reformulant ce théorème, nous obtenons ce qui suit si les nombres UN, X Et à positif et une ≠ 1, Que:

      Logarithme du quotient deux nombres positifs est égal à la différence entre les logarithmes du dividende et du diviseur. Pour le dire autrement, si les chiffres UN, X Et à positif et une ≠ 1, Que:

      Appliquons les théorèmes ci-dessus pour résoudre exemples:

      Si les chiffres X Et à sont négatifs, alors formule du logarithme du produit devient dénué de sens. Ainsi, il est interdit d'écrire :

      puisque les expressions log 2 (-8) et log 2 (-4) ne sont pas du tout définies (fonction logarithmique à= journal 2 X défini uniquement pour les valeurs d'argument positives X).

      Théorème du produit applicable non seulement pour deux, mais aussi pour un nombre illimité de facteurs. Cela signifie que pour chaque naturel k et tous les nombres positifs X 1 , X 2 , . . . ,xn il y a une identité :

      Depuis théorème du quotient du logarithme Une autre propriété du logarithme peut être obtenue. Il est de notoriété publique que le journal un 1= 0, donc

      Cela signifie qu'il y a une égalité :

      Logarithmes de deux nombres réciproques pour la même raison, ils différeront les uns des autres uniquement par leur signe. Donc:

      Logarithme. Propriétés des logarithmes

      Logarithme. Propriétés des logarithmes

      Pensons à l'égalité. Faites-nous connaître les valeurs de et et nous voulons trouver la valeur de .

      Autrement dit, nous recherchons l'exposant par lequel nous devons l'armer pour obtenir .

      Laisser une variable peut prendre n'importe quelle valeur réelle, alors les restrictions suivantes sont imposées aux variables : o" title="a>o"/> , 1″ title="a1″/>, 0″ title="b>0″ />

      Si nous connaissons les valeurs de et et que nous sommes confrontés à la tâche de trouver l'inconnue, alors une opération mathématique est introduite à cet effet, appelée logarithme.

      Pour trouver la valeur que nous prenons logarithme d'un nombre Par base :

      Le logarithme d'un nombre par rapport à sa base est l'exposant auquel il doit être élevé pour obtenir.

      C'est identité logarithmique de base:

      o» titre=»a>o»/> , 1″ titre=»a1″/>, 0″ titre=»b>0″/>

      est essentiellement une notation mathématique définitions du logarithme.

      L'opération mathématique du logarithme est l'inverse de l'opération d'exponentiation, donc propriétés des logarithmes sont étroitement liés aux propriétés du degré.

      Listons les principaux propriétés des logarithmes:

      (o" title="a>o"/> , 1″ titre=»a1″/>, 0″ titre=»b>0″/>, 0,

      d>0″/>, 1″ title=”d1″/>

      4.

      5.

      Le groupe de propriétés suivant permet de représenter l'exposant d'une expression sous le signe du logarithme, ou se trouvant à la base du logarithme sous la forme d'un coefficient devant le signe du logarithme :

      6.

      7.

      8.

      9.

      Le groupe de formules suivant permet de passer d'un logarithme avec une base donnée à un logarithme avec une base arbitraire, et s'appelle formules de transition vers une nouvelle base:

      10.

      12. (corollaire de la propriété 11)

      Les trois propriétés suivantes ne sont pas bien connues, mais elles sont souvent utilisées lors de la résolution d'équations logarithmiques ou lors de la simplification d'expressions contenant des logarithmes :

      13.

      14.

      15.

      Cas spéciaux:

      — logarithme décimal

      — un algorithme naturel

      Lors de la simplification d'expressions contenant des logarithmes, une approche générale est utilisée :

      1. Présentation décimales sous la forme d'ordinaires.

      2. Numéros mixtes représentés comme des fractions impropres.

      3. On décompose les nombres à la base du logarithme et sous le signe du logarithme en facteurs simples.

      4. Nous essayons de réduire tous les logarithmes à la même base.

      5. Appliquez les propriétés des logarithmes.

      Regardons des exemples d'expressions simplificatrices contenant des logarithmes.

      Exemple 1.

      Calculer:

      Simplifions tous les exposants : notre tâche est de les réduire à des logarithmes dont la base est le même nombre que la base de l'exposant.

      ==(par propriété 7)=(par propriété 6) =

      Remplaçons les indicateurs que nous avons entrés dans l'expression originale. On a:

      Réponse : 5h25

      Exemple 2. Calculer :

      Réduisons tous les logarithmes à la base 6 (dans ce cas, les logarithmes du dénominateur de la fraction « migreront » vers le numérateur) :

      Décomposons les nombres sous le signe du logarithme en facteurs simples :

      Appliquons les propriétés 4 et 6 :

      Présentons le remplacement

      On a:

      Réponse 1

      Logarithme . Identité logarithmique de base.

      Propriétés des logarithmes. Logarithme décimal. Un algorithme naturel.

      Logarithme nombre positif N en base (b > 0, b 1) est l'exposant x auquel b doit être élevé pour obtenir N .

      Cette entrée est équivalente à ce qui suit : bx = N .

      Exemples : log 3 81 = 4, puisque 3 4 = 81 ;

      journal 1/3 27 = – 3, puisque (1/3) - 3 = 3 3 = 27.

      La définition ci-dessus du logarithme peut s'écrire sous la forme d'une identité :

      Propriétés de base des logarithmes.

      2) log 1 = 0, puisque b 0 = 1 .

      3) Le logarithme du produit est égal à la somme des logarithmes des facteurs :

      4) Le logarithme du quotient est égal à la différence entre les logarithmes du dividende et du diviseur :

      5) Le logarithme d'une puissance est égal au produit de l'exposant et du logarithme de sa base :

      La conséquence de cette propriété est la suivante : logarithme de la racine égal au logarithme du nombre radical divisé par la puissance de la racine :

      6) Si la base du logarithme est un degré, alors la valeur l'inverse de l'exposant peut être extrait sous forme de rime logarithmique :

      Les deux dernières propriétés peuvent être combinées en une seule :

      7) Formule du module de transition (c'est-à-dire transition d'une base de logarithme à une autre base) :

      Dans le cas particulier où N=a nous avons:

      Logarithme décimal appelé logarithme de base 10. Il est désigné lg, c'est-à-dire journal 10 N= journal N. Logarithmes des nombres 10, 100, 1000, . p valent respectivement 1, 2, 3,…, c'est-à-dire j'ai tellement de positif

      unités, combien y a-t-il de zéros dans un nombre logarithmique après un. Logarithmes des nombres 0,1, 0,01, 0,001, . p valent respectivement –1, –2, –3,…, c'est-à-dire avoir autant de uns négatifs qu'il y a de zéros dans le nombre logarithmique précédant un (y compris les entiers nuls). Les logarithmes d'autres nombres ont une partie fractionnaire appelée mantisse. La partie entière d'un logarithme s'appelle caractéristique. Pour une utilisation pratique, les logarithmes décimaux sont les plus pratiques.

      Un algorithme naturel appelé logarithme de base e. Il est noté ln, c'est-à-dire enregistrer e N= journal N. Nombre e est irrationnel, sa valeur approximative est 2,718281828. C'est la limite vers laquelle tend le nombre (1 + 1 / n) n avec augmentation illimitée n(cm. première limite merveilleuse sur la page "Limites" séquences de nombres»).
      Aussi étrange que cela puisse paraître, les logarithmes naturels se sont révélés très pratiques pour effectuer divers types d'opérations liées à l'analyse des fonctions. Calculer des logarithmes à la base e effectué beaucoup plus rapidement que pour toute autre raison.

    • Que faut-il aujourd’hui pour adopter un enfant en Russie ? L'adoption en Russie, en plus d'une décision personnelle responsable, implique un certain nombre de procédures de vérification par l'État des candidats. Une sélection rigoureuse dès la phase préparatoire contribue à plus […]
    • Informations gratuites sur le TIN ou l'OGRN du registre des impôts dans toute la Russie - en ligne Sur le portail des services fiscaux unifiés, vous pouvez obtenir des informations sur enregistrement d'état entités juridiques, entrepreneurs individuels, […]
    • Sanction pour conduite sans papiers (permis de conduire, assurance, STS) Parfois, par oubli, les conducteurs prennent le volant sans permis et reçoivent une amende pour conduite sans papiers. Nous vous rappelons qu’un passionné d’automobile doit avoir […]
    • Fleurs pour hommes. Quelles fleurs peut-on offrir à un homme ? Quelles fleurs peut-on offrir à un homme ? Il n’y a pas beaucoup de fleurs « mâles », mais il y en a quelques-unes qui sont offertes aux hommes. Une petite liste de fleurs devant vous : les chrysanthèmes.
    • Des roses. Oeillets.
    • […]
    • Un mémo interne est une forme spéciale de document utilisé dans l'environnement interne d'une entreprise et sert à résoudre rapidement les problèmes de production actuels. Généralement, ce document est rédigé dans le but de présenter certains […]
    • Quand et comment percevoir la partie capitalisée de votre pension de la Sberbank ? La Sberbank est une banque partenaire du fonds de pension de l'État. Sur cette base, les citoyens inscrits à une pension par capitalisation pourraient transférer la partie capitalisée […] Allocations familiales à Oulianovsk et dans la région d'Oulianovsk en 2018. De plus, des programmes approuvés par la législation fédérale fonctionnent dans toutes les régions. Voyons qui peut compter sur quels avantages. Comment les autorités régionales […] Guide détaillé comment rédiger une procuration pour représenter les intérêts