Γενική άποψη συστημάτων γραμμικών εξισώσεων. Επίλυση συστημάτων γραμμικών αλγεβρικών εξισώσεων, μέθοδοι επίλυσης, παραδείγματα

28.09.2019

Η επίλυση συστημάτων γραμμικών αλγεβρικών εξισώσεων (SLAE) είναι αναμφίβολα το πιο σημαντικό θέμα σε ένα μάθημα γραμμικής άλγεβρας. Μεγάλο ποσόπροβλήματα από όλους τους κλάδους των μαθηματικών ανάγονται στην επίλυση συστημάτων γραμμικές εξισώσεις. Αυτοί οι παράγοντες εξηγούν τον λόγο για αυτό το άρθρο. Το υλικό του άρθρου είναι επιλεγμένο και δομημένο έτσι ώστε με τη βοήθειά του να μπορείτε

μαζεύω βέλτιστη μέθοδοςλύσεις στο σύστημα γραμμικών αλγεβρικών εξισώσεων σας,
μελέτη της θεωρίας της επιλεγμένης μεθόδου,
λύστε το σύστημα γραμμικών εξισώσεων σας εξετάζοντας λεπτομερείς λύσεις σε τυπικά παραδείγματα και προβλήματα.

Σύντομη περιγραφή του υλικού του άρθρου.

Αρχικά, δίνουμε όλους τους απαραίτητους ορισμούς, έννοιες και εισάγουμε σημειώσεις.

Στη συνέχεια, θα εξετάσουμε μεθόδους για την επίλυση συστημάτων γραμμικών αλγεβρικών εξισώσεων στα οποία ο αριθμός των εξισώσεων είναι ίσος με τον αριθμό των άγνωστων μεταβλητών και οι οποίες έχουν μια μοναδική λύση. Πρώτον, θα επικεντρωθούμε στη μέθοδο Cramer, δεύτερον, θα δείξουμε τη μέθοδο μήτρας για την επίλυση τέτοιων συστημάτων εξισώσεων, τρίτον, θα αναλύσουμε τη μέθοδο Gauss (μέθοδος διαδοχική εξάλειψηάγνωστες μεταβλητές). Για να εμπεδώσουμε τη θεωρία, σίγουρα θα λύσουμε πολλά SLAE με διαφορετικούς τρόπους.

Μετά από αυτό, θα προχωρήσουμε στην επίλυση συστημάτων γραμμικών αλγεβρικών εξισώσεων γενικής μορφής, στα οποία ο αριθμός των εξισώσεων δεν συμπίπτει με τον αριθμό των άγνωστων μεταβλητών ή ο κύριος πίνακας του συστήματος είναι ενικός. Ας διατυπώσουμε το θεώρημα Kronecker-Capelli, το οποίο μας επιτρέπει να καθορίσουμε τη συμβατότητα των SLAE. Ας αναλύσουμε τη λύση των συστημάτων (εάν είναι συμβατά) χρησιμοποιώντας την έννοια του ελάσσονος βάσης ενός πίνακα. Θα εξετάσουμε επίσης τη μέθοδο Gauss και θα περιγράψουμε λεπτομερώς τις λύσεις στα παραδείγματα.

Σίγουρα θα σταθούμε στη δομή της γενικής λύσης ομοιογενών και ανομοιογενών συστημάτων γραμμικών αλγεβρικών εξισώσεων. Ας δώσουμε την έννοια ενός θεμελιώδους συστήματος λύσεων και ας δείξουμε πώς γράφεται η γενική λύση ενός SLAE χρησιμοποιώντας τα διανύσματα του θεμελιώδους συστήματος λύσεων. Για καλύτερη κατανόησηΑς δούμε μερικά παραδείγματα.

Συμπερασματικά, θα εξετάσουμε συστήματα εξισώσεων που μπορούν να αναχθούν σε γραμμικά, καθώς και διάφορα προβλήματα στην επίλυση των οποίων προκύπτουν SLAE.

Πλοήγηση στη σελίδα.

Ορισμοί, έννοιες, προσδιορισμοί.

Θα εξετάσουμε συστήματα p γραμμικών αλγεβρικών εξισώσεων με n άγνωστες μεταβλητές (το p μπορεί να είναι ίσο με n) της μορφής

Άγνωστες μεταβλητές, - συντελεστές (μερικοί πραγματικοί ή μιγαδικοί αριθμοί), - ελεύθεροι όροι (επίσης πραγματικοί ή μιγαδικοί αριθμοί).

Αυτή η μορφή εγγραφής SLAE ονομάζεται συντεταγμένη.

ΣΕ μορφή μήτρας Η γραφή αυτού του συστήματος εξισώσεων έχει τη μορφή,
Οπου - ο κύριος πίνακας του συστήματος, - ένας πίνακας στήλης άγνωστων μεταβλητών, - ένας πίνακας στήλης ελεύθερων όρων.

Αν προσθέσουμε μια μήτρα-στήλη ελεύθερων όρων στον πίνακα Α ως (n+1)η στήλη, παίρνουμε το λεγόμενο εκτεταμένη μήτρασυστήματα γραμμικών εξισώσεων. Συνήθως, ένας εκτεταμένος πίνακας συμβολίζεται με το γράμμα T και η στήλη των ελεύθερων όρων χωρίζεται με μια κάθετη γραμμή από τις υπόλοιπες στήλες, δηλαδή

Επίλυση συστήματος γραμμικών αλγεβρικών εξισώσεωνονομάζεται ένα σύνολο τιμών άγνωστων μεταβλητών που μετατρέπει όλες τις εξισώσεις του συστήματος σε ταυτότητες. Η εξίσωση μήτρας για δεδομένες τιμές των άγνωστων μεταβλητών γίνεται επίσης ταυτότητα.

Εάν ένα σύστημα εξισώσεων έχει τουλάχιστον μία λύση, τότε ονομάζεται άρθρωση.

Εάν ένα σύστημα εξισώσεων δεν έχει λύσεις, τότε ονομάζεται μη άρθρωση.

Εάν ένα SLAE έχει μια μοναδική λύση, τότε ονομάζεται βέβαιος; αν υπάρχουν περισσότερες από μία λύσεις, τότε - αβέβαιος.

Αν οι ελεύθεροι όροι όλων των εξισώσεων του συστήματος είναι ίσοι με μηδέν , τότε καλείται το σύστημα ομοιογενής, σε διαφορετική περίπτωση - ετερογενής.

Επίλυση στοιχειωδών συστημάτων γραμμικών αλγεβρικών εξισώσεων.

Εάν ο αριθμός των εξισώσεων ενός συστήματος είναι ίσος με τον αριθμό των άγνωστων μεταβλητών και η ορίζουσα του κύριου πίνακα του δεν είναι ίση με μηδέν, τότε τέτοια SLAE θα ονομάζονται στοιχειώδης. Τέτοια συστήματα εξισώσεων έχουν μια μοναδική λύση και στην περίπτωση ενός ομοιογενούς συστήματος, όλες οι άγνωστες μεταβλητές είναι ίσες με μηδέν.

Αρχίσαμε να μελετάμε τέτοια SLAE Λύκειο. Όταν τα λύναμε, πήραμε μια εξίσωση, εκφράσαμε μια άγνωστη μεταβλητή ως προς τις άλλες και την αντικαταστήσαμε στις υπόλοιπες εξισώσεις, μετά πήραμε την επόμενη εξίσωση, εκφράσαμε την επόμενη άγνωστη μεταβλητή και την αντικαταστήσαμε με άλλες εξισώσεις κ.ο.κ. Ή χρησιμοποίησαν τη μέθοδο της πρόσθεσης, δηλαδή πρόσθεσαν δύο ή περισσότερες εξισώσεις για να εξαλείψουν κάποιες άγνωστες μεταβλητές. Δεν θα σταθούμε λεπτομερώς σε αυτές τις μεθόδους, αφού ουσιαστικά αποτελούν τροποποιήσεις της μεθόδου Gauss.

Οι κύριες μέθοδοι επίλυσης στοιχειωδών συστημάτων γραμμικών εξισώσεων είναι η μέθοδος Cramer, η μέθοδος matrix και η μέθοδος Gauss. Ας τα τακτοποιήσουμε.

Επίλυση συστημάτων γραμμικών εξισώσεων με τη μέθοδο του Cramer.

Ας υποθέσουμε ότι πρέπει να λύσουμε ένα σύστημα γραμμικών αλγεβρικών εξισώσεων

στις οποίες ο αριθμός των εξισώσεων είναι ίσος με τον αριθμό των άγνωστων μεταβλητών και η ορίζουσα του κύριου πίνακα του συστήματος είναι διαφορετική από το μηδέν, δηλαδή .

Έστω η ορίζουσα του κύριου πίνακα του συστήματος, και - ορίζουσες πινάκων που λαμβάνονται από το Α με αντικατάσταση 1ος, 2ος,…, ντοςστήλη αντίστοιχα στη στήλη των ελεύθερων μελών:

Με αυτόν τον συμβολισμό, οι άγνωστες μεταβλητές υπολογίζονται χρησιμοποιώντας τους τύπους της μεθόδου Cramer ως . Έτσι βρίσκεται η λύση σε ένα σύστημα γραμμικών αλγεβρικών εξισώσεων με τη μέθοδο του Cramer.

Παράδειγμα.

Η μέθοδος του Cramer .

Λύση.

Η κύρια μήτρα του συστήματος έχει τη μορφή . Ας υπολογίσουμε τον προσδιοριστικό του παράγοντα (αν χρειάζεται, βλέπε το άρθρο):

Δεδομένου ότι η ορίζουσα του κύριου πίνακα του συστήματος είναι μη μηδενική, το σύστημα έχει μια μοναδική λύση που μπορεί να βρεθεί με τη μέθοδο του Cramer.

Ας συνθέσουμε και ας υπολογίσουμε τις απαραίτητες ορίζουσες (λαμβάνουμε την ορίζουσα αντικαθιστώντας την πρώτη στήλη στον πίνακα Α με μια στήλη ελεύθερων όρων, την ορίζουσα αντικαθιστώντας τη δεύτερη στήλη με μια στήλη ελεύθερων όρων και αντικαθιστώντας την τρίτη στήλη του πίνακα Α με μια στήλη ελεύθερων όρων) :

Εύρεση άγνωστων μεταβλητών με χρήση τύπων :

Απάντηση:

Το κύριο μειονέκτημα της μεθόδου του Cramer (αν μπορεί να ονομαστεί μειονέκτημα) είναι η πολυπλοκότητα του υπολογισμού των οριζόντων όταν ο αριθμός των εξισώσεων στο σύστημα είναι μεγαλύτερος από τρεις.

Επίλυση συστημάτων γραμμικών αλγεβρικών εξισώσεων με τη μέθοδο του πίνακα (με χρήση αντίστροφου πίνακα).

Έστω ένα σύστημα γραμμικών αλγεβρικών εξισώσεων που δίνεται σε μορφή πίνακα, όπου ο πίνακας A έχει διάσταση n επί n και η ορίζουσά του είναι μη μηδενική.

Εφόσον , ο πίνακας Α είναι αντιστρέψιμος, δηλαδή υπάρχει ένας αντίστροφος πίνακας. Αν πολλαπλασιάσουμε και τις δύο πλευρές της ισότητας με τα αριστερά, παίρνουμε έναν τύπο για την εύρεση μιας μήτρας-στήλης άγνωστων μεταβλητών. Έτσι αποκτήσαμε μια λύση σε ένα σύστημα γραμμικών αλγεβρικών εξισώσεων χρησιμοποιώντας τη μέθοδο του πίνακα.

Παράδειγμα.

Επίλυση συστήματος γραμμικών εξισώσεων μέθοδος μήτρας.

Λύση.

Ας ξαναγράψουμε το σύστημα εξισώσεων σε μορφή πίνακα:

Επειδή

τότε το SLAE μπορεί να λυθεί χρησιμοποιώντας τη μέθοδο matrix. Χρησιμοποιώντας τον αντίστροφο πίνακα, η λύση σε αυτό το σύστημα μπορεί να βρεθεί ως .

Ας κατασκευάσουμε έναν αντίστροφο πίνακα χρησιμοποιώντας έναν πίνακα από αλγεβρικές προσθήκες στοιχείων του πίνακα Α (αν χρειάζεται, δείτε το άρθρο):

Απομένει να υπολογιστεί ο πίνακας άγνωστων μεταβλητών πολλαπλασιάζοντας τον αντίστροφο πίνακα σε μια μήτρα-στήλη ελεύθερων μελών (αν είναι απαραίτητο, δείτε το άρθρο):

Απάντηση:

ή σε άλλη σημειογραφία x 1 = 4, x 2 = 0, x 3 = -1.

Το κύριο πρόβλημα κατά την εύρεση λύσεων σε συστήματα γραμμικών αλγεβρικών εξισώσεων χρησιμοποιώντας τη μέθοδο του πίνακα είναι η πολυπλοκότητα της εύρεσης του αντίστροφου πίνακα, ειδικά για τετράγωνους πίνακες τάξης υψηλότερης από την τρίτη.

Επίλυση συστημάτων γραμμικών εξισώσεων με τη μέθοδο Gauss.

Ας υποθέσουμε ότι πρέπει να βρούμε μια λύση σε ένα σύστημα n γραμμικών εξισώσεων με n άγνωστες μεταβλητές
η ορίζουσα του κύριου πίνακα του οποίου είναι διαφορετική από το μηδέν.

Η ουσία της μεθόδου Gaussαποτελείται από διαδοχική εξαίρεση άγνωστων μεταβλητών: πρώτον, το x 1 εξαιρείται από όλες τις εξισώσεις του συστήματος, ξεκινώντας από τη δεύτερη, μετά το x 2 εξαιρείται από όλες τις εξισώσεις, ξεκινώντας από την τρίτη και ούτω καθεξής, μέχρι μόνο η άγνωστη μεταβλητή x n παραμένει στην τελευταία εξίσωση. Αυτή η διαδικασία μετασχηματισμού εξισώσεων συστήματος για διαδοχική εξάλειψη άγνωστων μεταβλητών ονομάζεται άμεση Gaussian μέθοδος. Μετά την ολοκλήρωση της εμπρόσθιας διαδρομής της μεθόδου Gauss, το x n βρίσκεται από την τελευταία εξίσωση, χρησιμοποιώντας αυτήν την τιμή από την προτελευταία εξίσωση, υπολογίζεται το x n-1 και ούτω καθεξής, το x 1 βρίσκεται από την πρώτη εξίσωση. Ονομάζεται η διαδικασία υπολογισμού άγνωστων μεταβλητών κατά τη μετάβαση από την τελευταία εξίσωση του συστήματος στην πρώτη αντίστροφη της μεθόδου Gauss.

Ας περιγράψουμε εν συντομία τον αλγόριθμο για την εξάλειψη άγνωστων μεταβλητών.

Θα υποθέσουμε ότι , αφού μπορούμε πάντα να το πετύχουμε αυτό ανταλλάσσοντας τις εξισώσεις του συστήματος. Ας εξαλείψουμε την άγνωστη μεταβλητή x 1 από όλες τις εξισώσεις του συστήματος, ξεκινώντας από τη δεύτερη. Για να γίνει αυτό, στη δεύτερη εξίσωση του συστήματος προσθέτουμε την πρώτη, πολλαπλασιαζόμενη με , στην τρίτη εξίσωση προσθέτουμε την πρώτη, πολλαπλασιαζόμενη με , και ούτω καθεξής, στην nη εξίσωση προσθέτουμε την πρώτη, πολλαπλασιαζόμενη με . Το σύστημα των εξισώσεων μετά από τέτοιους μετασχηματισμούς θα πάρει τη μορφή

πού και .

Θα είχαμε φτάσει στο ίδιο αποτέλεσμα αν είχαμε εκφράσει x 1 ως προς άλλες άγνωστες μεταβλητές στην πρώτη εξίσωση του συστήματος και αντικαθιστούσαμε την έκφραση που προκύπτει με όλες τις άλλες εξισώσεις. Έτσι, η μεταβλητή x 1 εξαιρείται από όλες τις εξισώσεις, ξεκινώντας από τη δεύτερη.

Στη συνέχεια, προχωράμε με παρόμοιο τρόπο, αλλά μόνο με μέρος του προκύπτοντος συστήματος, το οποίο σημειώνεται στο σχήμα

Για να γίνει αυτό, στην τρίτη εξίσωση του συστήματος προσθέτουμε τη δεύτερη, πολλαπλασιαζόμενη με , στην τέταρτη εξίσωση προσθέτουμε τη δεύτερη, πολλαπλασιαζόμενη με , και ούτω καθεξής, στην nη εξίσωση προσθέτουμε τη δεύτερη, πολλαπλασιαζόμενη με . Το σύστημα των εξισώσεων μετά από τέτοιους μετασχηματισμούς θα πάρει τη μορφή

πού και . Έτσι, η μεταβλητή x 2 εξαιρείται από όλες τις εξισώσεις, ξεκινώντας από την τρίτη.

Στη συνέχεια, προχωράμε στην εξάλειψη του αγνώστου x 3 και ενεργούμε παρόμοια με το τμήμα του συστήματος που σημειώνεται στο σχήμα

Συνεχίζουμε λοιπόν την άμεση εξέλιξη της μεθόδου Gauss μέχρι το σύστημα να πάρει τη μορφή

Από αυτή τη στιγμή ξεκινάμε το αντίστροφο της μεθόδου Gauss: υπολογίζουμε το x n από την τελευταία εξίσωση καθώς, χρησιμοποιώντας την τιμή του x n που προκύπτει, βρίσκουμε x n-1 από την προτελευταία εξίσωση, και ούτω καθεξής, βρίσκουμε x 1 από την πρώτη εξίσωση .

Παράδειγμα.

Επίλυση συστήματος γραμμικών εξισώσεων Μέθοδος Gauss.

Λύση.

Ας εξαιρέσουμε την άγνωστη μεταβλητή x 1 από τη δεύτερη και τρίτη εξίσωση του συστήματος. Για να γίνει αυτό, και στις δύο πλευρές της δεύτερης και τρίτης εξίσωσης προσθέτουμε τα αντίστοιχα μέρη της πρώτης εξίσωσης, πολλαπλασιαζόμενα επί και επί, αντίστοιχα:

Τώρα αφαιρούμε το x 2 από την τρίτη εξίσωση προσθέτοντας στην αριστερή και δεξιά πλευρά της την αριστερή και τη δεξιά πλευρά της δεύτερης εξίσωσης, πολλαπλασιαζόμενη επί:

Αυτό ολοκληρώνει την εμπρός διαδρομή της μεθόδου Gauss, ξεκινάμε την αντίστροφη διαδρομή.

Από την τελευταία εξίσωση του προκύπτοντος συστήματος εξισώσεων βρίσκουμε το x 3:

Από τη δεύτερη εξίσωση παίρνουμε .

Από την πρώτη εξίσωση βρίσκουμε την υπόλοιπη άγνωστη μεταβλητή και έτσι συμπληρώνουμε το αντίστροφο της μεθόδου Gauss.

Απάντηση:

X 1 = 4, x 2 = 0, x 3 = -1.

Επίλυση συστημάτων γραμμικών αλγεβρικών εξισώσεων γενικής μορφής.

Γενικά, ο αριθμός των εξισώσεων του συστήματος p δεν συμπίπτει με τον αριθμό των άγνωστων μεταβλητών n:

Τέτοια SLAE μπορεί να μην έχουν λύσεις, να έχουν μία μόνο λύση ή να έχουν άπειρες λύσεις. Αυτή η δήλωση ισχύει επίσης για συστήματα εξισώσεων των οποίων ο κύριος πίνακας είναι τετράγωνος και ενικός.

Θεώρημα Kronecker–Capelli.

Πριν βρεθεί μια λύση σε ένα σύστημα γραμμικών εξισώσεων, είναι απαραίτητο να εξακριβωθεί η συμβατότητά του. Η απάντηση στο ερώτημα πότε το SLAE είναι συμβατό και πότε είναι ασυνεπές δίνεται από Θεώρημα Kronecker–Capelli:
Για να είναι συνεπές ένα σύστημα p εξισώσεων με n αγνώστους (το p μπορεί να είναι ίσο με n), είναι απαραίτητο και αρκετό η κατάταξη του κύριου πίνακα του συστήματος να είναι ίση με την κατάταξη του εκτεταμένου πίνακα, δηλαδή , Rank(A)=Rank(T).

Ας εξετάσουμε, ως παράδειγμα, την εφαρμογή του θεωρήματος Kronecker–Capelli για τον προσδιορισμό της συμβατότητας ενός συστήματος γραμμικών εξισώσεων.

Παράδειγμα.

Βρείτε αν το σύστημα γραμμικών εξισώσεων έχει λύσεις.

Λύση.

. Ας χρησιμοποιήσουμε τη μέθοδο της οριοθέτησης ανηλίκων. Ανήλικο δεύτερης τάξης διαφορετικό από το μηδέν. Ας δούμε τους ανηλίκους τρίτης τάξης που το συνορεύουν:

Δεδομένου ότι όλα τα συνοριακά ανήλικα της τρίτης τάξης είναι ίσα με μηδέν, η κατάταξη του κύριου πίνακα είναι ίση με δύο.

Με τη σειρά του, η κατάταξη του εκτεταμένου πίνακα ισούται με τρία, αφού το δευτερεύον είναι τρίτης τάξης

διαφορετικό από το μηδέν.

Ετσι, Rang(A), επομένως, χρησιμοποιώντας το θεώρημα Kronecker–Capelli, μπορούμε να συμπεράνουμε ότι το αρχικό σύστημα γραμμικών εξισώσεων είναι ασυνεπές.

Απάντηση:

Το σύστημα δεν έχει λύσεις.

Έτσι, μάθαμε να καθορίζουμε την ασυνέπεια ενός συστήματος χρησιμοποιώντας το θεώρημα Kronecker–Capelli.

Αλλά πώς να βρεθεί μια λύση σε ένα SLAE εάν διαπιστωθεί η συμβατότητά του;

Για να γίνει αυτό, χρειαζόμαστε την έννοια του ελάσσονος βάσης ενός πίνακα και ένα θεώρημα για την κατάταξη ενός πίνακα.

Ο ελάσσονας της υψηλότερης τάξης του πίνακα Α, διαφορετικός από το μηδέν, ονομάζεται βασικός.

Από τον ορισμό μιας ελάσσονος βάσης προκύπτει ότι η σειρά της είναι ίση με την κατάταξη του πίνακα. Για έναν μη μηδενικό πίνακα Α μπορεί να υπάρχουν πολλά ελάσσονα βάσης.

Για παράδειγμα, εξετάστε τη μήτρα .

Όλα τα δευτερεύοντα στοιχεία τρίτης τάξης αυτού του πίνακα είναι ίσα με μηδέν, αφού τα στοιχεία της τρίτης σειράς αυτού του πίνακα είναι το άθροισμα των αντίστοιχων στοιχείων της πρώτης και της δεύτερης σειράς.

Τα παρακάτω δευτερεύοντα δευτερεύοντα είναι βασικά, αφού είναι μη μηδενικά

Ανήλικοι δεν είναι βασικές, αφού είναι ίσες με μηδέν.

Θεώρημα κατάταξης πίνακα.

Εάν η κατάταξη ενός πίνακα της τάξης p επί n είναι ίση με r, τότε όλα τα στοιχεία σειρών (και στηλών) του πίνακα που δεν αποτελούν το επιλεγμένο βασικό ελάσσονα εκφράζονται γραμμικά ως προς τα στοιχεία της αντίστοιχης γραμμής (και στήλης) που σχηματίζουν το βασικό ελάσσονα.

Τι μας λέει το θεώρημα κατάταξης του πίνακα;

Εάν, σύμφωνα με το θεώρημα Kronecker-Capelli, έχουμε καθορίσει τη συμβατότητα του συστήματος, τότε επιλέγουμε οποιαδήποτε βασική ελάσσονα του κύριου πίνακα του συστήματος (η σειρά του είναι ίση με r) και αποκλείουμε από το σύστημα όλες τις εξισώσεις που κάνουν δεν αποτελούν την επιλεγμένη βάση ελάσσονος σημασίας. Το SLAE που λαμβάνεται με αυτόν τον τρόπο θα είναι ισοδύναμο με το αρχικό, καθώς οι εξισώσεις που απορρίπτονται εξακολουθούν να είναι περιττές (σύμφωνα με το θεώρημα κατάταξης του πίνακα, είναι ένας γραμμικός συνδυασμός των υπόλοιπων εξισώσεων).

Ως αποτέλεσμα, μετά την απόρριψη περιττών εξισώσεων του συστήματος, είναι δυνατές δύο περιπτώσεις.

Εάν ο αριθμός των εξισώσεων r στο προκύπτον σύστημα είναι ίσος με τον αριθμό των άγνωστων μεταβλητών, τότε θα είναι οριστικός και η μόνη λύση μπορεί να βρεθεί με τη μέθοδο Cramer, τη μέθοδο matrix ή τη μέθοδο Gauss.

Παράδειγμα.

Λύση.

Κατάταξη του κύριου πίνακα του συστήματος ισούται με δύο, αφού το δευτερεύον είναι δεύτερης τάξης διαφορετικό από το μηδέν. Extended Matrix Rank ισούται επίσης με δύο, αφού το μόνο δευτερεύον τρίτης τάξης είναι μηδέν

και η δευτερεύουσας τάξης δευτερεύουσας σημασίας που εξετάστηκε παραπάνω είναι διαφορετική από το μηδέν. Με βάση το θεώρημα Kronecker–Capelli, μπορούμε να υποστηρίξουμε τη συμβατότητα του αρχικού συστήματος γραμμικών εξισώσεων, αφού Rank(A)=Rank(T)=2.

Ως δευτερεύουσα βάση παίρνουμε . Σχηματίζεται από τους συντελεστές της πρώτης και δεύτερης εξίσωσης:

Η τρίτη εξίσωση του συστήματος δεν συμμετέχει στον σχηματισμό της ελάσσονος βάσης, επομένως την αποκλείουμε από το σύστημα που βασίζεται στο θεώρημα για την κατάταξη του πίνακα:

Έτσι αποκτήσαμε ένα στοιχειώδες σύστημα γραμμικών αλγεβρικών εξισώσεων. Ας το λύσουμε χρησιμοποιώντας τη μέθοδο του Cramer:

Απάντηση:

x 1 = 1, x 2 = 2.

Αν ο αριθμός των εξισώσεων r στο SLAE που προκύπτει μικρότερος αριθμόςάγνωστες μεταβλητές n, στη συνέχεια στην αριστερή πλευρά των εξισώσεων αφήνουμε τους όρους που αποτελούν τη βάση ελάσσονος σημασίας και μεταφέρουμε τους υπόλοιπους όρους στις δεξιές πλευρές των εξισώσεων του συστήματος με το αντίθετο πρόσημο.

Οι άγνωστες μεταβλητές (r από αυτές) που παραμένουν στις αριστερές πλευρές των εξισώσεων καλούνται κύριος.

Οι άγνωστες μεταβλητές (υπάρχουν n - r κομμάτια) που βρίσκονται στις δεξιές πλευρές καλούνται Ελεύθερος.

Τώρα πιστεύουμε ότι οι ελεύθερες άγνωστες μεταβλητές μπορούν να λάβουν αυθαίρετες τιμές, ενώ οι r κύριες άγνωστες μεταβλητές θα εκφραστούν μέσω ελεύθερων άγνωστων μεταβλητών με μοναδικό τρόπο. Η έκφρασή τους μπορεί να βρεθεί λύνοντας το SLAE που προκύπτει χρησιμοποιώντας τη μέθοδο Cramer, τη μέθοδο matrix ή τη μέθοδο Gauss.

Ας το δούμε με ένα παράδειγμα.

Παράδειγμα.

Να λύσετε ένα σύστημα γραμμικών αλγεβρικών εξισώσεων .

Λύση.

Ας βρούμε την κατάταξη του κύριου πίνακα του συστήματος με τη μέθοδο της οριοθέτησης ανηλίκων. Ας πάρουμε ένα 1 1 = 1 ως μη μηδενικό δευτερεύον της πρώτης τάξης. Ας ξεκινήσουμε την αναζήτηση για ένα μη μηδενικό δευτερεύον της δεύτερης τάξης που συνορεύει με αυτό το δευτερεύον:

Έτσι βρήκαμε ένα μη μηδενικό μινόρε δεύτερης τάξης. Ας ξεκινήσουμε την αναζήτηση για ένα μη μηδενικό συνοριακό δευτερεύον της τρίτης τάξης:

Έτσι, η κατάταξη του κύριου πίνακα είναι τρεις. Η κατάταξη του εκτεταμένου πίνακα είναι επίσης ίση με τρία, δηλαδή το σύστημα είναι συνεπές.

Λαμβάνουμε ως βάση το μη μηδενικό δευτερεύον δευτερεύον της τρίτης τάξης.

Για λόγους σαφήνειας, δείχνουμε τα στοιχεία που αποτελούν τη βασική ελάσσονα:

Αφήνουμε τους όρους που εμπλέκονται στη βασική ελάσσονα στην αριστερή πλευρά των εξισώσεων του συστήματος και μεταφέρουμε τους υπόλοιπους με αντίθετα πρόσημα στις δεξιές πλευρές:

Ας δώσουμε στις ελεύθερες άγνωστες μεταβλητές x 2 και x 5 αυθαίρετες τιμές, δηλαδή αποδεχόμαστε , όπου υπάρχουν αυθαίρετοι αριθμοί. Σε αυτή την περίπτωση, η SLAE θα λάβει τη μορφή

Ας λύσουμε το προκύπτον στοιχειώδες σύστημα γραμμικών αλγεβρικών εξισώσεων χρησιμοποιώντας τη μέθοδο του Cramer:

Ως εκ τούτου, .

Στην απάντησή σας, μην ξεχάσετε να υποδείξετε δωρεάν άγνωστες μεταβλητές.

Απάντηση:

Πού είναι αυθαίρετοι αριθμοί.

Συνοψίζω.

Για να λύσουμε ένα σύστημα γενικών γραμμικών αλγεβρικών εξισώσεων, προσδιορίζουμε πρώτα τη συμβατότητά του χρησιμοποιώντας το θεώρημα Kronecker–Capelli. Εάν η κατάταξη του κύριου πίνακα δεν είναι ίση με την κατάταξη του εκτεταμένου πίνακα, τότε συμπεραίνουμε ότι το σύστημα είναι ασυμβίβαστο.

Εάν η κατάταξη του κύριου πίνακα είναι ίση με την κατάταξη του εκτεταμένου πίνακα, τότε επιλέγουμε ελάσσονα βάσης και απορρίπτουμε τις εξισώσεις του συστήματος που δεν συμμετέχουν στον σχηματισμό του επιλεγμένου βασικού ελάσσονος πίνακα.

Αν η σειρά του ελάσσονος βάσης ίσο με τον αριθμόάγνωστες μεταβλητές, τότε το SLAE έχει μια μοναδική λύση, την οποία βρίσκουμε με οποιαδήποτε γνωστή σε εμάς μέθοδο.

Εάν η σειρά του ελάσσονος βάσης είναι μικρότερη από τον αριθμό των άγνωστων μεταβλητών, τότε στην αριστερή πλευρά των εξισώσεων συστήματος αφήνουμε τους όρους με τις κύριες άγνωστες μεταβλητές, μεταφέρουμε τους υπόλοιπους όρους στις δεξιές πλευρές και δίνουμε αυθαίρετες τιμές σε τις δωρεάν άγνωστες μεταβλητές. Από το προκύπτον σύστημα γραμμικών εξισώσεων βρίσκουμε τους κύριους αγνώστους μεταβλητές κατά μέθοδο Cramer, μέθοδος matrix ή μέθοδος Gaussian.

Μέθοδος Gauss για την επίλυση συστημάτων γραμμικών αλγεβρικών εξισώσεων γενικής μορφής.

Η μέθοδος Gauss μπορεί να χρησιμοποιηθεί για την επίλυση συστημάτων γραμμικών αλγεβρικών εξισώσεων οποιουδήποτε είδους χωρίς πρώτα να ελεγχθεί η συνοχή τους. Η διαδικασία διαδοχικής εξάλειψης άγνωστων μεταβλητών καθιστά δυνατή την εξαγωγή συμπερασμάτων τόσο για τη συμβατότητα όσο και για την ασυμβατότητα του SLAE, και εάν υπάρχει λύση, καθιστά δυνατή την εύρεση της.

Από υπολογιστική άποψη, η μέθοδος Gauss είναι προτιμότερη.

Δες το Λεπτομερής περιγραφήκαι ανέλυσε παραδείγματα στο άρθρο η μέθοδος Gauss για την επίλυση συστημάτων γραμμικών αλγεβρικών εξισώσεων γενικής μορφής.

Γράψτε μια γενική λύση σε ομοιογενή και ανομοιογενή γραμμικά αλγεβρικά συστήματα χρησιμοποιώντας διανύσματα του θεμελιώδους συστήματος λύσεων.

Στην ενότητα αυτή θα μιλήσουμε για ταυτόχρονα ομοιογενή και ανομοιογενή συστήματα γραμμικών αλγεβρικών εξισώσεων που έχουν άπειρο αριθμό λύσεων.

Ας ασχοληθούμε πρώτα με τα ομοιογενή συστήματα.

Βασικό σύστημα λύσεωνομοιογενές σύστημα p γραμμικών αλγεβρικών εξισώσεων με n άγνωστες μεταβλητές είναι μια συλλογή από (n – r) γραμμικά ανεξάρτητες λύσεις αυτού του συστήματος, όπου r είναι η τάξη του βασικού ελάσσονος του κύριου πίνακα του συστήματος.

Αν υποδηλώσουμε γραμμικά ανεξάρτητες λύσεις ενός ομοιογενούς SLAE ως X (1) , X (2) , ..., X (n-r) (X (1) , X (2) , ..., X (n-r) είναι στηλώδεις πίνακες διαστάσεων n επί 1), τότε η γενική λύση αυτού του ομοιογενούς συστήματος παριστάνεται ως γραμμικός συνδυασμός διανυσμάτων του θεμελιώδους συστήματος λύσεων με αυθαίρετους σταθερούς συντελεστές C 1, C 2, ..., C (n-r), που είναι, .

Τι σημαίνει ο όρος γενική λύση ενός ομοιογενούς συστήματος γραμμικών αλγεβρικών εξισώσεων (οροσλάου);

Το νόημα είναι απλό: ο τύπος καθορίζει όλες τις πιθανές λύσεις του αρχικού SLAE, με άλλα λόγια, λαμβάνοντας οποιοδήποτε σύνολο τιμών αυθαίρετων σταθερών C 1, C 2, ..., C (n-r), χρησιμοποιώντας τον τύπο που θα λάβετε ένα από τα διαλύματα του αρχικού ομοιογενούς SLAE.

Έτσι, εάν βρούμε ένα θεμελιώδες σύστημα λύσεων, τότε μπορούμε να ορίσουμε όλες τις λύσεις αυτού του ομοιογενούς SLAE ως .

Ας δείξουμε τη διαδικασία κατασκευής ενός θεμελιώδους συστήματος λύσεων σε ένα ομοιογενές SLAE.

Επιλέγουμε το βασικό μινόρε του αρχικού συστήματος γραμμικών εξισώσεων, αποκλείουμε όλες τις άλλες εξισώσεις από το σύστημα και μεταφέρουμε όλους τους όρους που περιέχουν ελεύθερες άγνωστες μεταβλητές στη δεξιά πλευρά των εξισώσεων του συστήματος με αντίθετα πρόσημα. Ας δώσουμε στις ελεύθερες άγνωστες μεταβλητές τις τιμές 1,0,0,...,0 και ας υπολογίσουμε τους κύριους αγνώστους λύνοντας το προκύπτον στοιχειώδες σύστημα γραμμικών εξισώσεων με οποιονδήποτε τρόπο, για παράδειγμα, χρησιμοποιώντας τη μέθοδο Cramer. Αυτό θα έχει ως αποτέλεσμα το X (1) - την πρώτη λύση του θεμελιώδους συστήματος. Αν δώσεις δωρεάν άγνωστες τιμές 0,1,0,0,…,0 και υπολογίστε τους κύριους αγνώστους, παίρνουμε Χ (2) . Και ούτω καθεξής. Αν αντιστοιχίσουμε τις τιμές 0,0,...,0,1 στις ελεύθερες άγνωστες μεταβλητές και υπολογίσουμε τις κύριες άγνωστες, λαμβάνουμε X (n-r) . Με αυτόν τον τρόπο, θα κατασκευαστεί ένα θεμελιώδες σύστημα λύσεων σε ένα ομοιογενές SLAE και η γενική του λύση μπορεί να γραφτεί με τη μορφή .

Για ανομοιογενή συστήματα γραμμικών αλγεβρικών εξισώσεων, η γενική λύση παριστάνεται με τη μορφή , όπου είναι η γενική λύση του αντίστοιχου ομοιογενούς συστήματος και είναι η συγκεκριμένη λύση του αρχικού ανομοιογενούς SLAE, την οποία λαμβάνουμε δίνοντας στους ελεύθερους αγνώστους τις τιμές 0,0,…,0 και υπολογισμός των τιμών των κύριων αγνώστων.

Ας δούμε παραδείγματα.

Παράδειγμα.

Να βρείτε το θεμελιώδες σύστημα λύσεων και τη γενική λύση ενός ομοιογενούς συστήματος γραμμικών αλγεβρικών εξισώσεων .

Λύση.

Η κατάταξη του κύριου πίνακα ομοιογενών συστημάτων γραμμικών εξισώσεων είναι πάντα ίση με την κατάταξη του εκτεταμένου πίνακα. Ας βρούμε την κατάταξη του κύριου πίνακα χρησιμοποιώντας τη μέθοδο της οριοθέτησης ανηλίκων. Ως μη μηδενικό ελάσσονα πρώτης τάξης, παίρνουμε το στοιχείο a 1 1 = 9 του κύριου πίνακα του συστήματος. Ας βρούμε τη συνοριακή μη μηδενική ελάσσονα δεύτερης τάξης:

Βρέθηκε ανήλικο δεύτερης τάξης, διαφορετικό από το μηδέν. Ας περάσουμε από τα ανήλικα τρίτης τάξης που το συνορεύουν σε αναζήτηση ενός μη μηδενικού:

Όλοι οι ανήλικοι που συνορεύουν τρίτης τάξης είναι ίσοι με μηδέν, επομένως, η κατάταξη του κύριου και του εκτεταμένου πίνακα είναι ίση με δύο. Ας πάρουμε . Για λόγους σαφήνειας, ας σημειώσουμε τα στοιχεία του συστήματος που το σχηματίζουν:

Η τρίτη εξίσωση του αρχικού SLAE δεν συμμετέχει στον σχηματισμό του ελάσσονος βάσης, επομένως, μπορεί να αποκλειστεί:

Αφήνουμε τους όρους που περιέχουν τους κύριους αγνώστους στις δεξιές πλευρές των εξισώσεων και μεταφέρουμε τους όρους με ελεύθερους αγνώστους στις δεξιές πλευρές:

Ας κατασκευάσουμε ένα θεμελιώδες σύστημα λύσεων στο αρχικό ομοιογενές σύστημα γραμμικών εξισώσεων. Το θεμελιώδες σύστημα λύσεων αυτού του SLAE αποτελείται από δύο λύσεις, αφού το αρχικό SLAE περιέχει τέσσερις άγνωστες μεταβλητές και η τάξη του βασικού του δευτερεύοντος είναι ίση με δύο. Για να βρούμε το X (1), δίνουμε στις ελεύθερες άγνωστες μεταβλητές τις τιμές x 2 = 1, x 4 = 0, μετά βρίσκουμε τους κύριους αγνώστους από το σύστημα εξισώσεων
.

Σύστημα m γραμμικών εξισώσεων με n αγνώστουςονομάζεται σύστημα της μορφής

Οπου ένα ijΚαι β i (Εγώ=1,…,Μ; σι=1,…,n) είναι κάποιοι γνωστοί αριθμοί, και x 1,…,x n– άγνωστο. Στον προσδιορισμό των συντελεστών ένα ijπρώτος δείκτης Εγώδηλώνει τον αριθμό της εξίσωσης, και το δεύτερο ι– ο αριθμός του αγνώστου στον οποίο βρίσκεται αυτός ο συντελεστής.

Θα γράψουμε τους συντελεστές για τους αγνώστους με τη μορφή πίνακα , που θα καλέσουμε μήτρα του συστήματος.

Οι αριθμοί στη δεξιά πλευρά των εξισώσεων είναι b 1,…,b mλέγονται ελεύθερα μέλη.

Ολότητα nαριθμοί c 1 ,…,c nπου ονομάζεται απόφασηενός δεδομένου συστήματος, αν κάθε εξίσωση του συστήματος γίνεται ισότητα μετά την αντικατάσταση αριθμών σε αυτήν c 1 ,…,c nαντί των αντίστοιχων αγνώστων x 1,…,x n.

Το καθήκον μας θα είναι να βρούμε λύσεις στο σύστημα. Σε αυτήν την περίπτωση, μπορεί να προκύψουν τρεις καταστάσεις:

Ένα σύστημα γραμμικών εξισώσεων που έχει τουλάχιστον μία λύση ονομάζεται άρθρωση. Διαφορετικά, δηλ. αν το σύστημα δεν έχει λύσεις, τότε καλείται μη άρθρωση.

Ας εξετάσουμε τρόπους για να βρούμε λύσεις στο σύστημα.

ΜΕΘΟΔΟΣ ΜΗΤΡΩΝ ΕΠΙΛΥΣΗΣ ΣΥΣΤΗΜΑΤΩΝ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ

Οι πίνακες καθιστούν δυνατή τη σύντομη εγγραφή ενός συστήματος γραμμικών εξισώσεων. Έστω ένα σύστημα 3 εξισώσεων με τρεις αγνώστους:

Εξετάστε τη μήτρα του συστήματος 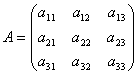και πίνακες στήλες αγνώστων και ελεύθερων όρων

Ας βρούμε τη δουλειά

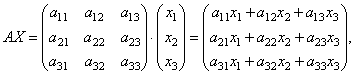
εκείνοι. Ως αποτέλεσμα του γινόμενου, λαμβάνουμε τις αριστερές πλευρές των εξισώσεων αυτού του συστήματος. Στη συνέχεια, χρησιμοποιώντας τον ορισμό της ισότητας πίνακα, αυτό το σύστημα μπορεί να γραφτεί στη μορφή

ή μικρότερη ΕΝΑ∙X=B.

Εδώ είναι οι πίνακες ΕΝΑΚαι σιείναι γνωστά, και η μήτρα Χάγνωστος. Είναι απαραίτητο να το βρείτε, γιατί... τα στοιχεία του είναι η λύση σε αυτό το σύστημα. Αυτή η εξίσωση ονομάζεται εξίσωση μήτρας.

Έστω η ορίζουσα μήτρας διαφορετική από το μηδέν | ΕΝΑ| ≠ 0. Τότε η εξίσωση του πίνακα λύνεται ως εξής. Πολλαπλασιάστε και τις δύο πλευρές της εξίσωσης στα αριστερά με τον πίνακα Α'1, αντίστροφο του πίνακα ΕΝΑ: . Επειδή η Α -1 Α = ΕΚαι μι∙Χ = Χ, τότε λαμβάνουμε μια λύση στην εξίσωση του πίνακα στη μορφή X = A -1 B .

Σημειώστε ότι εφόσον ο αντίστροφος πίνακας μπορεί να βρεθεί μόνο για τετραγωνικούς πίνακες, η μέθοδος του πίνακα μπορεί να λύσει μόνο εκείνα τα συστήματα στα οποία ο αριθμός των εξισώσεων συμπίπτει με τον αριθμό των αγνώστων. Ωστόσο, η καταγραφή μήτρας του συστήματος είναι επίσης δυνατή στην περίπτωση που ο αριθμός των εξισώσεων δεν είναι ίσος με τον αριθμό των αγνώστων, τότε ο πίνακας ΕΝΑδεν θα είναι τετράγωνο και επομένως είναι αδύνατο να βρεθεί λύση στο σύστημα στη μορφή X = A -1 B.

Παραδείγματα.Επίλυση συστημάτων εξισώσεων.

ΚΑΝΟΝΑΣ ΚΡΑΜΕΡ

Θεωρήστε ένα σύστημα 3 γραμμικών εξισώσεων με τρεις άγνωστους:

Ορίζουσα τρίτης τάξης που αντιστοιχεί στον πίνακα συστήματος, δηλ. που αποτελείται από συντελεστές για αγνώστους,

που ονομάζεται καθοριστικό στοιχείο του συστήματος.

Ας συνθέσουμε τρεις ακόμη ορίζουσες ως εξής: αντικαταστήστε διαδοχικά 1, 2 και 3 στήλες στην ορίζουσα D με μια στήλη ελεύθερων όρων

Τότε μπορούμε να αποδείξουμε το ακόλουθο αποτέλεσμα.

Θεώρημα (κανόνας Cramer).Αν η ορίζουσα του συστήματος Δ ≠ 0, τότε το εξεταζόμενο σύστημα έχει μία και μόνο μία λύση, και

Απόδειξη. Ας εξετάσουμε λοιπόν ένα σύστημα 3 εξισώσεων με τρεις αγνώστους. Ας πολλαπλασιάσουμε την 1η εξίσωση του συστήματος με το αλγεβρικό συμπλήρωμα Α 11στοιχείο ένα 11, 2η εξίσωση – on Α 21και 3η – στις Α 31:

Ας προσθέσουμε αυτές τις εξισώσεις:

Ας δούμε κάθε μία από τις αγκύλες και τη δεξιά πλευρά αυτής της εξίσωσης. Με το θεώρημα για την επέκταση της ορίζουσας σε στοιχεία της 1ης στήλης

Ομοίως, μπορεί να αποδειχθεί ότι και .

Τέλος, είναι εύκολο να το παρατηρήσετε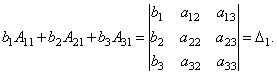

Έτσι, παίρνουμε την ισότητα: .

Ως εκ τούτου, .

Οι ισότητες και προκύπτουν ομοίως, από τις οποίες προκύπτει η δήλωση του θεωρήματος.

Έτσι, σημειώνουμε ότι αν η ορίζουσα του συστήματος Δ ≠ 0, τότε το σύστημα έχει μοναδική λύση και το αντίστροφο. Αν η ορίζουσα του συστήματος είναι ίση με μηδέν, τότε το σύστημα είτε έχει άπειρο αριθμό λύσεων είτε δεν έχει λύσεις, δηλ. ασύμβατες.

Παραδείγματα.Επίλυση συστήματος εξισώσεων

ΜΕΘΟΔΟΣ GAUSS

Οι μέθοδοι που συζητήθηκαν προηγουμένως μπορούν να χρησιμοποιηθούν για την επίλυση μόνο εκείνων των συστημάτων στα οποία ο αριθμός των εξισώσεων συμπίπτει με τον αριθμό των αγνώστων και η ορίζουσα του συστήματος πρέπει να είναι διαφορετική από το μηδέν. Η μέθοδος Gauss είναι πιο καθολική και κατάλληλη για συστήματα με οποιοδήποτε αριθμό εξισώσεων. Συνίσταται στη συνεπή εξάλειψη αγνώστων από τις εξισώσεις του συστήματος.

Εξετάστε ξανά ένα σύστημα τριών εξισώσεων με τρεις αγνώστους:

Θα αφήσουμε την πρώτη εξίσωση αμετάβλητη και από τη 2η και την 3η θα εξαιρέσουμε τους όρους που περιέχουν x 1. Για να γίνει αυτό, διαιρέστε τη δεύτερη εξίσωση με ΕΝΑ 21 και πολλαπλασιάστε με - ΕΝΑ 11 και μετά προσθέστε το στην 1η εξίσωση. Ομοίως, διαιρούμε την τρίτη εξίσωση με ΕΝΑ 31 και πολλαπλασιάστε με – ΕΝΑ 11 και μετά προσθέστε το με το πρώτο. Ως αποτέλεσμα, το αρχικό σύστημα θα έχει τη μορφή:

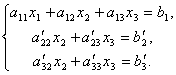
Τώρα από την τελευταία εξίσωση εξαλείφουμε τον όρο που περιέχει x 2. Για να το κάνετε αυτό, διαιρέστε την τρίτη εξίσωση με, πολλαπλασιάστε με και προσθέστε με τη δεύτερη. Τότε θα έχουμε ένα σύστημα εξισώσεων:

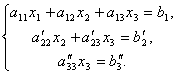
Από εδώ, από την τελευταία εξίσωση είναι εύκολο να βρεθεί x 3, τότε από τη 2η εξίσωση x 2και τέλος, από 1η - x 1.

Όταν χρησιμοποιείται η μέθοδος Gaussian, οι εξισώσεις μπορούν να αντικατασταθούν εάν είναι απαραίτητο.

Συχνά, αντί να γράφουν ένα νέο σύστημα εξισώσεων, περιορίζονται στο να γράψουν τον εκτεταμένο πίνακα του συστήματος:

και στη συνέχεια να το φέρει σε τριγωνική ή διαγώνια μορφή χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς.

ΠΡΟΣ ΤΗΝ στοιχειώδεις μεταμορφώσειςΟι πίνακες περιλαμβάνουν τους ακόλουθους μετασχηματισμούς:

αναδιάταξη σειρών ή στηλών.
πολλαπλασιασμός μιας συμβολοσειράς με έναν αριθμό διαφορετικό από το μηδέν.
προσθέτοντας άλλες γραμμές σε μια γραμμή.

Παραδείγματα:Επίλυση συστημάτων εξισώσεων με τη μέθοδο Gauss.

Έτσι, το σύστημα έχει άπειρο αριθμό λύσεων.

Ορισμός.Σύστημα Μεξισώσεις με n άγνωστους σε γενική εικόναγράφεται ως εξής:

Οπου ένα ijείναι οι συντελεστές, και β i– μόνιμη.

Οι λύσεις του συστήματος είναι nαριθμοί που, όταν αντικαθίστανται στο σύστημα, μετατρέπουν κάθε εξίσωσή του σε ταυτότητα.

Ορισμός.Εάν ένα σύστημα έχει τουλάχιστον μία λύση, τότε ονομάζεται άρθρωση. Εάν ένα σύστημα δεν έχει μια ενιαία λύση, τότε ονομάζεται ασυνεπές.

Ορισμός.Ένα σύστημα ονομάζεται προσδιορισμένο αν έχει μόνο μία λύση και αόριστο εάν έχει περισσότερες από μία.

Ορισμός.Για ένα σύστημα γραμμικών εξισώσεων ο πίνακας

Α = ονομάζεται μήτρα του συστήματος, και μήτρα

A * = που ονομάζεται εκτεταμένη μήτρα του συστήματος

Ορισμός.Αν b 1 , b 2 , …,b m = 0, τότε το σύστημα ονομάζεται ομοιογενές. Σχόλιο.Ένα ομοιογενές σύστημα είναι πάντα συνεπές, γιατί έχει πάντα μηδενική λύση.

Στοιχειώδεις μετασχηματισμοί συστημάτων.

1. Προσθέτοντας και στις δύο πλευρές της μιας εξίσωσης τα αντίστοιχα μέρη της άλλης, πολλαπλασιασμένα με τον ίδιο αριθμό, όχι ίσο με το μηδέν.

2. Αναδιάταξη εξισώσεων.

3. Αφαίρεση από το σύστημα εξισώσεων που είναι ταυτότητες για όλους Χ.

Οι τύποι του Cramer.

Αυτή η μέθοδος εφαρμόζεται επίσης μόνο στην περίπτωση συστημάτων γραμμικών εξισώσεων, όπου ο αριθμός των μεταβλητών συμπίπτει με τον αριθμό των εξισώσεων.

Θεώρημα.Σύστημα n εξισώσεων με n αγνώστους

εάν η ορίζουσα του πίνακα συστήματος δεν είναι ίση με μηδέν, τότε το σύστημα έχει μια μοναδική λύση και αυτή η λύση βρίσκεται χρησιμοποιώντας τους τύπους: x i =Οπου D = det A, ΕΝΑ D iείναι ο προσδιοριστής του πίνακα που λαμβάνεται από τον πίνακα συστήματος αντικαθιστώντας τη στήλη Εγώστήλη ελεύθερων μελών β i.

D i =

Παράδειγμα.Βρείτε τη λύση στο σύστημα των εξισώσεων:

D = = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;

D 1 = = (28 – 48) – (42 – 32) = -20 – 10 = -30.

D 2 = = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.

D 3 = = 5(32 – 42) + (16 – 56) = -50 – 40 = -90.

Σημείωση 1.Εάν το σύστημα είναι ομοιογενές, π.χ. b i = 0, τότε για το D¹0 το σύστημα έχει μια μοναδική λύση μηδέν x 1 = x 2 = … = x n = 0.

Σημείωση 2.Στο D=0το σύστημα έχει άπειρο αριθμό λύσεων.

Μέθοδος αντίστροφης μήτρας.

Η μέθοδος του πίνακα εφαρμόζεται στην επίλυση συστημάτων εξισώσεων όπου ο αριθμός των εξισώσεων είναι ίσος με τον αριθμό των αγνώστων.

Ας δοθεί το σύστημα των εξισώσεων: Ας δημιουργήσουμε πίνακες:

Α= - πίνακας συντελεστών για μεταβλητές ή πίνακας του συστήματος.

B = - πίνακας - στήλη ελεύθερων όρων.

X = - πίνακας - στήλη αγνώστων.

Τότε το σύστημα των εξισώσεων μπορεί να γραφτεί: A×X = B.Ας πολλαπλασιάσουμε και τις δύο πλευρές της ισότητας από τα αριστερά με A -1: A -1 ×A×X = A -1 ×B, επειδή A -1 ×A = E,Οτι Ε×Χ = Α -1 ×Β, τότε ισχύει ο ακόλουθος τύπος:

X = A -1 ×B

Έτσι, για να εφαρμοστεί αυτή η μέθοδος είναι απαραίτητο να βρεθεί αντίστροφη μήτρα.

Παράδειγμα.Λύστε το σύστημα των εξισώσεων:

X = , B = , A =

Ας βρούμε τον αντίστροφο πίνακα A -1.

D = det A = 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30≠0 ⇒ υπάρχει ο αντίστροφος πίνακας.

Μ 11 = ; Μ 21 = ; Μ 31 = ;

M 12 = M 22 = M 32 =

M 13 = M 23 = M 33 =

Α -1 = ;

Ας ελέγξουμε:

A×A -1 =
=Ε.

Εύρεση του πίνακα X.

X = = A -1 B = × = .

Λάβαμε τις λύσεις συστήματος: x =1; y = 2; z = 3.

4.Μέθοδος Gauss.

Ας δοθεί το σύστημα Μγραμμικές εξισώσεις με nάγνωστος:

Υποθέτοντας ότι ο συντελεστής στο σύστημα έναΤο 11 είναι διαφορετικό από το μηδέν (αν δεν συμβαίνει αυτό, τότε η εξίσωση με μη μηδενικό συντελεστή στο Χ 1). Μετασχηματίζουμε το σύστημα ως εξής: αφήνουμε την πρώτη εξίσωση αμετάβλητη και αποκλείουμε το άγνωστο από όλες τις άλλες εξισώσεις Χ 1 χρησιμοποιώντας ισοδύναμους μετασχηματισμούς με τον τρόπο που περιγράφεται παραπάνω.

Στο προκύπτον σύστημα

υποθέτοντας ότι (το οποίο μπορεί πάντα να ληφθεί με αναδιάταξη εξισώσεων ή όρων εντός εξισώσεων), αφήνουμε τις δύο πρώτες εξισώσεις του συστήματος αμετάβλητες και από τις υπόλοιπες εξισώσεις, χρησιμοποιώντας τη δεύτερη εξίσωση, εξαλείφουμε το άγνωστο με τη βοήθεια στοιχειωδών μετασχηματισμών Χ 2. Στο νέο σύστημα που παραλήφθηκε

αρκεί να αφήσουμε τις τρεις πρώτες εξισώσεις αμετάβλητες και από όλες τις άλλες, χρησιμοποιώντας την τρίτη εξίσωση, εξαλείφουμε το άγνωστο με στοιχειώδεις μετασχηματισμούς Χ 3 .

Αυτή η διαδικασία συνεχίζεται μέχρι να συμβεί μία από τις τρεις πιθανές περιπτώσεις:

1) εάν ως αποτέλεσμα καταλήξουμε σε ένα σύστημα, μία από τις εξισώσεις του οποίου έχει μηδενικούς συντελεστές για όλους τους αγνώστους και έναν μη μηδενικό ελεύθερο όρο, τότε το αρχικό σύστημα είναι ασυνεπές.

2) εάν ως αποτέλεσμα μετασχηματισμών λάβουμε ένα σύστημα με τριγωνικό πίνακα συντελεστών, τότε το σύστημα είναι συνεπές και καθορισμένο.

3) εάν ληφθεί ένα σταδιακό σύστημα συντελεστών (και δεν πληρούται η προϋπόθεση του σημείου 1), τότε το σύστημα είναι συνεπές και αόριστο.

Θεωρήστε το τετράγωνο σύστημα : (1)

Αυτό το σύστημα έχει έναν συντελεστή έναΤο 11 είναι διαφορετικό από το μηδέν. Εάν αυτή η προϋπόθεση δεν πληρούνταν, τότε για να την αποκτήσετε, θα ήταν απαραίτητο να αναδιατάξετε τις εξισώσεις, βάζοντας πρώτα την εξίσωση της οποίας ο συντελεστής είναι ΧΤο 1 δεν είναι ίσο με μηδέν.

Θα πραγματοποιήσουμε τους ακόλουθους μετασχηματισμούς συστήματος:

1) επειδή ένα 11 ¹0, αφήνουμε την πρώτη εξίσωση αμετάβλητη.

2) αντί για τη δεύτερη εξίσωση, γράφουμε την εξίσωση που προκύπτει αν αφαιρέσουμε την πρώτη πολλαπλασιασμένη επί 4 από τη δεύτερη εξίσωση.

3) αντί για την τρίτη εξίσωση, γράφουμε τη διαφορά μεταξύ της τρίτης και της πρώτης, πολλαπλασιαζόμενη επί 3.

4) αντί για την τέταρτη εξίσωση, γράφουμε τη διαφορά μεταξύ της τέταρτης και της πρώτης, πολλαπλασιαζόμενη επί 5.

Ελήφθη νέο σύστημαείναι ισοδύναμη με την αρχική και έχει μηδενικούς συντελεστές σε όλες τις εξισώσεις εκτός από την πρώτη Χ 1 (αυτός ήταν ο σκοπός των μετασχηματισμών 1 – 4): (2)

Για τον παραπάνω μετασχηματισμό και για όλους τους περαιτέρω μετασχηματισμούς, δεν θα πρέπει να ξαναγράψετε εντελώς ολόκληρο το σύστημα, όπως μόλις έγινε. Το αρχικό σύστημα μπορεί να αναπαρασταθεί ως μήτρα

. (3)

Ο πίνακας (3) ονομάζεται εκτεταμένη μήτραγια το αρχικό σύστημα εξισώσεων. Εάν αφαιρέσουμε τη στήλη των ελεύθερων όρων από τον εκτεταμένο πίνακα, παίρνουμε πίνακας συντελεστών συστήματος, που μερικές φορές ονομάζεται απλώς μήτρα του συστήματος.

Το σύστημα (2) αντιστοιχεί στον εκτεταμένο πίνακα

Ας μετατρέψουμε αυτόν τον πίνακα ως εξής:

1) θα αφήσουμε τις δύο πρώτες γραμμές αμετάβλητες, αφού το στοιχείο έναΤο 22 δεν είναι μηδέν.

2) αντί για την τρίτη γραμμή, γράφουμε τη διαφορά μεταξύ της δεύτερης γραμμής και διπλασιάζουμε την τρίτη.

3) Αντικαταστήστε την τέταρτη γραμμή με τη διαφορά μεταξύ της δεύτερης γραμμής διπλασιασμένη και της τέταρτης γραμμής πολλαπλασιασμένη επί 5.

Το αποτέλεσμα είναι ένας πίνακας που αντιστοιχεί σε ένα σύστημα του οποίου το άγνωστο ΧΤο 1 εξαιρείται από όλες τις εξισώσεις εκτός από την πρώτη και το άγνωστο Χ 2 - από όλες τις εξισώσεις εκτός από την πρώτη και τη δεύτερη:

Τώρα ας αποκλείσουμε το άγνωστο Χ 3 από την τέταρτη εξίσωση. Για να γίνει αυτό, μετασχηματίζουμε τον τελευταίο πίνακα ως εξής:

1) θα αφήσουμε τις τρεις πρώτες γραμμές αμετάβλητες, αφού ένα 33¹0;

2) αντικαταστήστε την τέταρτη γραμμή με τη διαφορά μεταξύ της τρίτης, πολλαπλασιασμένης επί 39, και της τέταρτης: .

Η προκύπτουσα μήτρα αντιστοιχεί στο σύστημα

. (4)

Από την τελευταία εξίσωση αυτού του συστήματος προκύπτει Χ 4 = 2. Αντικαθιστώντας αυτήν την τιμή στην τρίτη εξίσωση, παίρνουμε Χ 3 = 3. Τώρα από τη δεύτερη εξίσωση προκύπτει ότι Χ 2 = 1, και από το πρώτο - Χ 1 = –1. Είναι προφανές ότι η λύση που προκύπτει είναι μοναδική (αφού η τιμή καθορίζεται με τον μόνο τρόπο Χ 4 τότε Χ 3, κλπ.).

Ορισμός:Ας ονομάσουμε έναν τετράγωνο πίνακα που έχει μη μηδενικούς αριθμούς στην κύρια διαγώνιο και μηδενικά κάτω από την κύρια διαγώνιο, τριγωνική μήτρα.

Ο πίνακας συντελεστών του συστήματος (4) είναι ένας τριγωνικός πίνακας.

Σχόλιο:Εάν, χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς, ο πίνακας των συντελεστών ενός τετραγωνικού συστήματος μπορεί να αναχθεί σε τριγωνικό πίνακα, τότε το σύστημα είναι συνεπές και καθορισμένο.

Ας δούμε ένα άλλο παράδειγμα: . (5)

Ας πραγματοποιήσουμε τους ακόλουθους μετασχηματισμούς του εκτεταμένου πίνακα του συστήματος:

1) αφήστε την πρώτη γραμμή αμετάβλητη.

2) αντί για τη δεύτερη γραμμή, γράψτε τη διαφορά μεταξύ της δεύτερης γραμμής και διπλασιάστε την πρώτη.

3) αντί για την τρίτη γραμμή, γράφουμε τη διαφορά μεταξύ της τρίτης γραμμής και τριπλασιάζουμε την πρώτη.

4) αντικαταστήστε την τέταρτη γραμμή με τη διαφορά μεταξύ της τέταρτης και της πρώτης.

5) Αντικαταστήστε την πέμπτη γραμμή με τη διαφορά της πέμπτης γραμμής και διπλασιάστε την πρώτη.

Ως αποτέλεσμα μετασχηματισμών, λαμβάνουμε τον πίνακα

Αφήνοντας τις δύο πρώτες σειρές αυτού του πίνακα αμετάβλητες, τον ανάγουμε στην ακόλουθη μορφή με στοιχειώδεις μετασχηματισμούς:

Αν τώρα, ακολουθώντας τη μέθοδο Gauss, που ονομάζεται και μέθοδος διαδοχικής εξάλειψης αγνώστων, χρησιμοποιώντας την τρίτη γραμμή φέρουμε τους συντελεστές στο Χ 3 στην τέταρτη και πέμπτη σειρά, μετά από τη διαίρεση όλων των στοιχείων της δεύτερης σειράς με το 5 και τη διαίρεση όλων των στοιχείων της τρίτης σειράς με το 2, λαμβάνουμε τον πίνακα

Κάθε μία από τις δύο τελευταίες σειρές αυτού του πίνακα αντιστοιχεί στην εξίσωση 0 Χ 1 +0Χ 2 +0Χ 3 +0Χ 4 +0Χ 5 = 0. Αυτή η εξίσωση ικανοποιείται από οποιοδήποτε σύνολο αριθμών Χ 1 ,Χ 2, ¼, Χ 5 και πρέπει να αφαιρεθεί από το σύστημα. Έτσι, το σύστημα με τον εκτεταμένο πίνακα που μόλις λήφθηκε είναι ισοδύναμο με ένα σύστημα με έναν εκτεταμένο πίνακα της μορφής

. (6)

Η τελευταία σειρά αυτού του πίνακα αντιστοιχεί στην εξίσωση
Χ 3 – 2Χ 4 + 3Χ 5 = –4. Αν είναι άγνωστο Χ 4 και Χ 5 δίνουν αυθαίρετες τιμές: Χ 4 = Γ 1; Χ 5 = Γ 2, τότε από την τελευταία εξίσωση του συστήματος που αντιστοιχεί στον πίνακα (6), προκύπτει Χ 3 = –4 + 2Γ 1 – 3Γ 2. Αντικατάσταση εκφράσεων Χ 3 ,Χ 4, και Χ 5 στη δεύτερη εξίσωση του ίδιου συστήματος, παίρνουμε Χ 2 = –3 + 2Γ 1 – 2Γ 2. Τώρα από την πρώτη εξίσωση μπορούμε να πάρουμε Χ 1 = 4 – Γ 1+ Γ 2. Η τελική λύση του συστήματος παρουσιάζεται στη φόρμα .

Θεωρήστε μια ορθογώνια μήτρα ΕΝΑ, του οποίου ο αριθμός στηλών Μπερισσότερο από τον αριθμό των γραμμών n. Μια τέτοια μήτρα ΕΝΑας καλέσουμε πάτησε.

Είναι προφανές ότι ο πίνακας (6) είναι ένας βηματικός πίνακας.

Εάν, κατά την εφαρμογή ισοδύναμων μετασχηματισμών σε ένα σύστημα εξισώσεων, τουλάχιστον μία εξίσωση ανάγεται στη μορφή

0Χ 1 + 0Χ 2 + ¼0 x n = β ι (β ι ¹ 0),

τότε το σύστημα είναι ασυμβίβαστο ή αντιφατικό, αφού ούτε ένα σύνολο αριθμών Χ 1 , Χ 2, ¼, x nδεν ικανοποιεί αυτή την εξίσωση.

Εάν, κατά τον μετασχηματισμό του εκτεταμένου πίνακα του συστήματος, ο πίνακας των συντελεστών μειωθεί σε σταδιακή μορφή και το σύστημα δεν αποδειχθεί ασυνεπές, τότε το σύστημα είναι συνεπές και αόριστο, δηλαδή έχει άπειρες λύσεις.

Στο τελευταίο σύστημα, όλες οι λύσεις μπορούν να ληφθούν με την ανάθεση συγκεκριμένων αριθμητικών τιμών στις παραμέτρους Γ 1Και Γ 2.

Ορισμός:Οι μεταβλητές των οποίων οι συντελεστές βρίσκονται στην κύρια διαγώνιο του πίνακα βημάτων (αυτό σημαίνει ότι αυτοί οι συντελεστές είναι διαφορετικοί από το μηδέν) ονομάζονται o κύριος. Στο παράδειγμα που συζητήθηκε παραπάνω, αυτά είναι τα άγνωστα Χ 1 , Χ 2 , Χ 3. Οι υπόλοιπες μεταβλητές καλούνται μη πυρήνα.Στο παραπάνω παράδειγμα, αυτές είναι οι μεταβλητές Χ 4, και Χ 5 . Στις μη κύριες μεταβλητές μπορούν να δοθούν οποιεσδήποτε τιμές ή να εκφραστούν μέσω παραμέτρων, όπως έγινε στο τελευταίο παράδειγμα.

Οι βασικές μεταβλητές εκφράζονται μοναδικά μέσω μη βασικών μεταβλητών.

Ορισμός:Εάν στις μη κύριες μεταβλητές δοθούν συγκεκριμένες αριθμητικές τιμές και οι κύριες μεταβλητές εκφράζονται μέσω αυτών, τότε η λύση που προκύπτει ονομάζεται ιδιωτική λύση.

Ορισμός:Εάν οι μη βασικές μεταβλητές εκφράζονται με όρους παραμέτρων, τότε προκύπτει μια λύση, η οποία ονομάζεται γενική λύση.

Ορισμός:Αν σε όλες τις δευτερεύουσες μεταβλητές δοθούν μηδενικές τιμές, τότε καλείται η λύση που προκύπτει βασικός.

Σχόλιο:Το ίδιο σύστημα μπορεί μερικές φορές να αναχθεί σε διαφορετικά σύνολα βασικών μεταβλητών. Έτσι, για παράδειγμα, μπορείτε να ανταλλάξετε την 3η και την 4η στήλη στον πίνακα (6). Τότε οι κύριες μεταβλητές θα είναι Χ 1 , Χ 2 ,Χ 4, και μη κύρια - Χ 3 και Χ 5 .

Ορισμός:Αν ληφθούν δύο διαφορετικά σύνολα βασικών μεταβλητών στο με διάφορους τρόπουςβρίσκοντας μια λύση στο ίδιο σύστημα, τότε αυτά τα σύνολα περιέχουν απαραίτητα τον ίδιο αριθμό μεταβλητών, που ονομάζονται κατάταξη συστήματος.

Ας εξετάσουμε ένα άλλο σύστημα που έχει άπειρες λύσεις: .

Ας μετατρέψουμε τον εκτεταμένο πίνακα του συστήματος χρησιμοποιώντας τη μέθοδο Gauss:

Όπως μπορείτε να δείτε, δεν λάβαμε έναν πίνακα βημάτων, αλλά ο τελευταίος πίνακας μπορεί να μετασχηματιστεί ανταλλάσσοντας την τρίτη και την τέταρτη στήλη: .

Αυτός ο πίνακας έχει ήδη βηματιστεί. Το αντίστοιχο σύστημα έχει δύο μη βασικές μεταβλητές - Χ 3 , Χ 5 και τρία κύρια - Χ 1 , Χ 2 , Χ 4 . Η λύση στο αρχικό σύστημα παρουσιάζεται με την ακόλουθη μορφή:

Ακολουθεί ένα παράδειγμα συστήματος που δεν έχει λύση:

Ας μετασχηματίσουμε τον πίνακα συστήματος χρησιμοποιώντας τη μέθοδο Gaussian:

Η τελευταία σειρά του τελευταίου πίνακα αντιστοιχεί στην άλυτη εξίσωση 0x 1 + 0x 2 + 0x 3 = 1. Κατά συνέπεια, το αρχικό σύστημα είναι ασυνεπές.

Διάλεξη Νο. 3.

Θέμα: Διανύσματα. Κλιμακωτό, διανυσματικό και μικτό γινόμενο διανυσμάτων

1. Η έννοια του διανύσματος. Συγγραμμικότητα, ορθογωνικότητα και συνεπίπεδη διανυσμάτων.

2. Γραμμική λειτουργία σε διανύσματα.

3. Scalar προϊόνδιανύσματα και η εφαρμογή του

4. Διάνυσμα έργα τέχνηςδιανύσματα και η εφαρμογή του

5. Μικτό γινόμενο διανυσμάτων και εφαρμογή του

1. Η έννοια του διανύσματος.

Ορισμός:Ένα διάνυσμα είναι ένα κατευθυνόμενο τμήμα με ένα σημείο έναρξης Α και ένα σημείο λήξης Β.

Ονομασία: , ,

Ορισμός:Το μήκος ή το μέτρο ενός διανύσματος ενός διανύσματος είναι ο αριθμός ίσο με μήκοςτμήμα AB που αντιπροσωπεύει ένα διάνυσμα.

Ορισμός:Ένα διάνυσμα ονομάζεται μηδέν εάν η αρχή και το τέλος του διανύσματος συμπίπτουν.

Ορισμός:Ένα διάνυσμα μοναδιαίου μήκους ονομάζεται μονάδα. Ορισμός:Τα διανύσματα ονομάζονται συγγραμμικά εάν βρίσκονται στην ίδια ευθεία ή σε παράλληλες ευθείες ( || ).

Σχόλιο:

1. Τα συγγραμμικά διανύσματα μπορούν να κατευθύνονται πανομοιότυπα ή αντίθετα.

2. Το μηδενικό διάνυσμα θεωρείται συγγραμμικό με οποιοδήποτε διάνυσμα.

Ορισμός:Δύο διανύσματα λέγονται ίσα αν είναι συγγραμμικά,

έχουν τις ίδιες κατευθύνσεις και τα ίδια μήκη ( = )

Σκοπός της υπηρεσίας. Η ηλεκτρονική αριθμομηχανή έχει σχεδιαστεί για να μελετά ένα σύστημα γραμμικών εξισώσεων. Συνήθως στη δήλωση προβλήματος πρέπει να βρείτε γενική και ειδική λύση του συστήματος. Κατά τη μελέτη συστημάτων γραμμικών εξισώσεων, επιλύονται τα ακόλουθα προβλήματα:

εάν το σύστημα είναι συνεργατικό.
εάν το σύστημα είναι συμβατό, τότε είναι οριστικό ή αόριστο (το κριτήριο για τη συμβατότητα του συστήματος καθορίζεται από το θεώρημα).
εάν το σύστημα έχει οριστεί, τότε πώς να βρεθεί η μοναδική του λύση (χρησιμοποιείται η μέθοδος Cramer, η μέθοδος αντίστροφης μήτρας ή η μέθοδος Jordan-Gauss).
εάν το σύστημα είναι αβέβαιο, τότε πώς να περιγράψετε το σύνολο των λύσεών του.

Ταξινόμηση συστημάτων γραμμικών εξισώσεων

Ένα αυθαίρετο σύστημα γραμμικών εξισώσεων έχει τη μορφή:
a 1 1 x 1 + a 1 2 x 2 + ... + a 1 n x n = b 1
a 2 1 x 1 + a 2 2 x 2 + ... + a 2 n x n = b 2
...................................................
a m 1 x 1 + a m 2 x 2 + ... + a m n x n = b m

Συστήματα γραμμικών ανομοιογενών εξισώσεων (ο αριθμός των μεταβλητών είναι ίσος με τον αριθμό των εξισώσεων, m = n).
Αυθαίρετα συστήματα γραμμικών ανομοιογενών εξισώσεων (m > n ή m< n).

Ορισμός. Λύση σε ένα σύστημα είναι κάθε σύνολο αριθμών c 1 ,c 2 ,...,c n , η αντικατάσταση των οποίων στο σύστημα αντί των αντίστοιχων αγνώστων μετατρέπει κάθε εξίσωση του συστήματος σε ταυτότητα.

Ορισμός. Δύο συστήματα λέγονται ισοδύναμα αν η λύση του πρώτου είναι η λύση του δεύτερου και το αντίστροφο.

Ορισμός. Ένα σύστημα που έχει τουλάχιστον μία λύση ονομάζεται άρθρωση. Ένα σύστημα που δεν έχει μια ενιαία λύση ονομάζεται ασυνεπές.

Ορισμός. Ένα σύστημα που έχει μια μοναδική λύση ονομάζεται βέβαιος, και η ύπαρξη περισσότερων από μία λύσεων είναι αβέβαιη.

Αλγόριθμος επίλυσης συστημάτων γραμμικών εξισώσεων

Βρείτε τις τάξεις των κύριων και εκτεταμένων πινάκων. Εάν δεν είναι ίσα, τότε σύμφωνα με το θεώρημα Kronecker-Capelli το σύστημα είναι ασυνεπές και εδώ τελειώνει η μελέτη.
Έστω rang(A) = rang(B) . Επιλέγουμε το βασικό δευτερεύον. Στην περίπτωση αυτή, όλα τα άγνωστα συστήματα γραμμικών εξισώσεων χωρίζονται σε δύο κατηγορίες. Οι άγνωστοι των οποίων οι συντελεστές περιλαμβάνονται στη βασική ελάσσονα ονομάζονται εξαρτημένες και οι άγνωστοι των οποίων οι συντελεστές δεν περιλαμβάνονται στη βασική ελάσσονα ονομάζονται ελεύθερες. Σημειώστε ότι η επιλογή των εξαρτημένων και ελεύθερων αγνώστων δεν είναι πάντα απλή.
Διαγράφουμε εκείνες τις εξισώσεις του συστήματος των οποίων οι συντελεστές δεν περιλαμβάνονται στη βασική ελάσσονα, αφού είναι συνέπειες των άλλων (σύμφωνα με το θεώρημα της ελάσσονος βάσης).
Μετακινούμε τους όρους των εξισώσεων που περιέχουν ελεύθερους αγνώστους στη δεξιά πλευρά. Ως αποτέλεσμα, παίρνουμε ένα σύστημα εξισώσεων r με r αγνώστους, ισοδύναμο με το δεδομένο, η ορίζουσα του οποίου είναι μη μηδενική.
Το σύστημα που προκύπτει επιλύεται με έναν από τους ακόλουθους τρόπους: τη μέθοδο Cramer, τη μέθοδο αντίστροφου πίνακα ή τη μέθοδο Jordan-Gauss. Βρίσκονται σχέσεις που εκφράζουν τις εξαρτημένες μεταβλητές μέσω των ελεύθερων.

Συνεχίζουμε να ασχολούμαστε με συστήματα γραμμικών εξισώσεων. Μέχρι στιγμής έχουμε εξετάσει συστήματα που έχουν μια μοναδική λύση. Τέτοια συστήματα μπορούν να επιλυθούν με οποιονδήποτε τρόπο: με μέθοδο αντικατάστασης("σχολείο"), σύμφωνα με τους τύπους του Cramer, μέθοδος μήτρας, Γκαουσιανή μέθοδος. Ωστόσο, στην πράξη, δύο ακόμη περιπτώσεις είναι ευρέως διαδεδομένες:

1) το σύστημα είναι ασυνεπές (δεν έχει λύσεις).

2) το σύστημα έχει άπειρες λύσεις.

Για αυτά τα συστήματα, χρησιμοποιείται η πιο καθολική από όλες τις μεθόδους λύσης - Γκαουσιανή μέθοδος. Στην πραγματικότητα, η μέθοδος του "σχολείου" θα οδηγήσει επίσης στην απάντηση, αλλά στα ανώτερα μαθηματικά συνηθίζεται να χρησιμοποιείται η μέθοδος Gaussian διαδοχικής εξάλειψης αγνώστων. Όσοι δεν είναι εξοικειωμένοι με τον αλγόριθμο της μεθόδου Gauss, παρακαλούμε να μελετήσουν πρώτα το μάθημα Γκαουσιανή μέθοδος

Οι ίδιοι οι μετασχηματισμοί στοιχειώδους πίνακα είναι ακριβώς οι ίδιοι, η διαφορά θα είναι στο τέλος της λύσης. Αρχικά, ας δούμε μερικά παραδείγματα όταν το σύστημα δεν έχει λύσεις (ασυνεπή).

Παράδειγμα 1

Τι τραβάει αμέσως την προσοχή σας σε αυτό το σύστημα; Ο αριθμός των εξισώσεων είναι μικρότερος από τον αριθμό των μεταβλητών. Υπάρχει ένα θεώρημα που λέει: «Αν ο αριθμός των εξισώσεων στο σύστημα είναι μικρότερος από τον αριθμό των μεταβλητών, τότε το σύστημα είτε είναι ασυνεπές είτε έχει άπειρες λύσεις».Και το μόνο που μένει είναι να μάθουμε.

Η αρχή της λύσης είναι εντελώς συνηθισμένη - γράφουμε τον εκτεταμένο πίνακα του συστήματος και, χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς, τον φέρνουμε σε μια σταδιακή μορφή:

(1). Στο επάνω αριστερό βήμα πρέπει να πάρουμε (+1) ή (–1). Δεν υπάρχουν τέτοιοι αριθμοί στην πρώτη στήλη, επομένως η αναδιάταξη των σειρών δεν θα κάνει τίποτα. Η μονάδα θα πρέπει να οργανωθεί μόνη της, και αυτό μπορεί να γίνει με διάφορους τρόπους. Το κάναμε αυτό. Στην πρώτη γραμμή προσθέτουμε την τρίτη γραμμή, πολλαπλασιαζόμενη επί (–1).

(2). Τώρα παίρνουμε δύο μηδενικά στην πρώτη στήλη. Στη δεύτερη γραμμή προσθέτουμε την πρώτη γραμμή, πολλαπλασιαζόμενη επί 3. Στην τρίτη γραμμή προσθέτουμε την πρώτη, πολλαπλασιαζόμενη επί 5.

(3). Μετά την ολοκλήρωση του μετασχηματισμού, είναι πάντα σκόπιμο να δούμε εάν είναι δυνατόν να απλοποιηθούν οι συμβολοσειρές που προκύπτουν; Μπορώ. Διαιρούμε τη δεύτερη γραμμή με το 2, παίρνοντας ταυτόχρονα την επιθυμητή (–1) στο δεύτερο βήμα. Διαιρέστε την τρίτη γραμμή με (–3).

(4). Προσθέστε μια δεύτερη γραμμή στην τρίτη γραμμή. Μάλλον όλοι παρατήρησαν την κακή γραμμή που προέκυψε από στοιχειώδεις μετασχηματισμούς:

. Είναι σαφές ότι αυτό δεν μπορεί να είναι έτσι.

Πράγματι, ας ξαναγράψουμε τον πίνακα που προκύπτει

πίσω στο σύστημα γραμμικών εξισώσεων:

Εάν, ως αποτέλεσμα στοιχειωδών μετασχηματισμών, λαμβάνεται μια συμβολοσειρά της φόρμας , Οπουλ είναι ένας αριθμός διαφορετικός από το μηδέν, τότε το σύστημα είναι ασυνεπές (δεν έχει λύσεις).

Πώς να γράψετε το τέλος μιας εργασίας; Πρέπει να γράψετε τη φράση:

«Ως αποτέλεσμα στοιχειωδών μετασχηματισμών, ελήφθη μια συμβολοσειρά της φόρμας, όπου λ ≠ 0 " Απάντηση: "Το σύστημα δεν έχει λύσεις (ασυνεπές)."

Σημειώστε ότι σε αυτή την περίπτωση δεν υπάρχει αντιστροφή του αλγόριθμου Gauss, δεν υπάρχουν λύσεις και απλά δεν υπάρχει τίποτα να βρείτε.

Παράδειγμα 2

Να λύσετε ένα σύστημα γραμμικών εξισώσεων

Αυτό είναι ένα παράδειγμα για να το λύσετε μόνοι σας. Πλήρης λύση και απάντηση στο τέλος του μαθήματος.

Σας υπενθυμίζουμε και πάλι ότι η λύση σας μπορεί να διαφέρει από τη λύση μας η μέθοδος Gauss δεν καθορίζει έναν σαφή αλγόριθμο και οι ίδιες οι ενέργειες πρέπει να μαντεύονται ανεξάρτητα.

Ένα άλλο τεχνικό χαρακτηριστικό της λύσης: οι στοιχειώδεις μετασχηματισμοί μπορούν να σταματήσουν Με τη μία, μόλις μια γραμμή όπως , όπου λ ≠ 0 . Ας εξετάσουμε ένα υπό όρους παράδειγμα: ας υποθέσουμε ότι μετά τον πρώτο μετασχηματισμό λαμβάνεται ο πίνακας

Αυτή η μήτρα δεν έχει ακόμη αναχθεί σε μορφή κλιμακίου, αλλά δεν υπάρχει ανάγκη για περαιτέρω στοιχειώδεις μετασχηματισμούς, αφού εμφανίστηκε μια γραμμή της φόρμας, όπου λ ≠ 0 . Θα πρέπει να δοθεί άμεσα η απάντηση ότι το σύστημα είναι ασυμβίβαστο.

Όταν ένα σύστημα γραμμικών εξισώσεων δεν έχει λύσεις, είναι σχεδόν δώρο στον μαθητή, λόγω του γεγονότος ότι επιτυγχάνεται μια σύντομη λύση, μερικές φορές κυριολεκτικά σε 2-3 βήματα. Αλλά τα πάντα σε αυτόν τον κόσμο είναι ισορροπημένα και ένα πρόβλημα στο οποίο το σύστημα έχει άπειρες λύσεις είναι απλώς μεγαλύτερο.

Παράδειγμα 3:

Να λύσετε ένα σύστημα γραμμικών εξισώσεων

Υπάρχουν 4 εξισώσεις και 4 άγνωστοι, οπότε το σύστημα μπορεί είτε να έχει μία μόνο λύση, είτε να μην έχει λύσεις, είτε να έχει άπειρες λύσεις. Όπως και να έχει, η μέθοδος Gauss θα μας οδηγήσει σε κάθε περίπτωση στην απάντηση. Αυτή είναι η ευελιξία του.

Η αρχή είναι και πάλι τυπική. Ας γράψουμε τον εκτεταμένο πίνακα του συστήματος και, χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς, ας τον φέρουμε σε μια σταδιακή μορφή:

Αυτό είναι όλο, και φοβήθηκες.

(1). Λάβετε υπόψη ότι όλοι οι αριθμοί στην πρώτη στήλη διαιρούνται με το 2, επομένως είμαστε ευχαριστημένοι με δύο στο επάνω αριστερό βήμα. Στη δεύτερη γραμμή προσθέτουμε την πρώτη γραμμή πολλαπλασιαζόμενη επί (–4). Στην τρίτη γραμμή προσθέτουμε την πρώτη γραμμή πολλαπλασιαζόμενη επί (–2). Στην τέταρτη γραμμή προσθέτουμε την πρώτη γραμμή, πολλαπλασιαζόμενη επί (–1).

Προσοχή!Πολλοί μπορεί να δελεαστούν από την τέταρτη γραμμή αφαιρώπρώτη γραμμή. Αυτό μπορεί να γίνει, αλλά δεν είναι απαραίτητο η εμπειρία δείχνει ότι η πιθανότητα λάθους στους υπολογισμούς αυξάνεται αρκετές φορές. Απλώς προσθέτουμε: στην τέταρτη γραμμή προσθέτουμε την πρώτη γραμμή, πολλαπλασιαζόμενη επί (–1) – ακριβώς!

(2). Οι τρεις τελευταίες γραμμές είναι αναλογικές, δύο από αυτές μπορούν να διαγραφούν. Εδώ πάλι πρέπει να δείξουμε αυξημένη προσοχή, αλλά είναι πραγματικά οι γραμμές ανάλογες; Για να είστε ασφαλείς, θα ήταν καλή ιδέα να πολλαπλασιάσετε τη δεύτερη γραμμή με (–1) και να διαιρέσετε την τέταρτη γραμμή με το 2, καταλήγοντας σε τρεις ίδιες γραμμές. Και μόνο μετά από αυτό αφαιρέστε δύο από αυτά. Ως αποτέλεσμα στοιχειωδών μετασχηματισμών, η εκτεταμένη μήτρα του συστήματος μειώνεται σε μια σταδιακή μορφή:

Όταν γράφετε μια εργασία σε ένα σημειωματάριο, συνιστάται να κάνετε τις ίδιες σημειώσεις με μολύβι για σαφήνεια.

Ας ξαναγράψουμε το αντίστοιχο σύστημα εξισώσεων:

Δεν υπάρχει καμία μυρωδιά μιας «συνηθισμένης» ενιαίας λύσης στο σύστημα εδώ. Κακή γραμμή πού λ ≠ 0, επίσης όχι. Αυτό σημαίνει ότι αυτή είναι η τρίτη περίπτωση που απομένει - το σύστημα έχει άπειρες λύσεις.

Ένα άπειρο σύνολο λύσεων σε ένα σύστημα γράφεται εν συντομία με τη μορφή του λεγόμενου γενική λύση του συστήματος.

Κοινή απόφασηθα βρούμε το σύστημα χρησιμοποιώντας το αντίστροφο της μεθόδου Gauss. Για συστήματα εξισώσεων με άπειρο σύνολο λύσεων, εμφανίζονται νέες έννοιες: "βασικές μεταβλητές"Και "ελεύθερες μεταβλητές". Πρώτα ας ορίσουμε ποιες μεταβλητές έχουμε βασικόςκαι ποιες μεταβλητές - Ελεύθερος. Δεν είναι απαραίτητο να εξηγήσουμε λεπτομερώς τους όρους της γραμμικής άλγεβρας, αρκεί να θυμόμαστε ότι υπάρχουν και τέτοιοι βασικές μεταβλητέςΚαι δωρεάν μεταβλητές.

Οι βασικές μεταβλητές «κάθονται» πάντα αυστηρά στα βήματα του πίνακα. ΣΕ σε αυτό το παράδειγμαοι βασικές μεταβλητές είναι Χ 1 και Χ 3 .

Οι δωρεάν μεταβλητές είναι το παν παραμένωνμεταβλητές που δεν έλαβαν βήμα. Στην περίπτωσή μας υπάρχουν δύο από αυτά: Χ 2 και Χ 4 – ελεύθερες μεταβλητές.

Τώρα χρειάζεστε Ολαβασικές μεταβλητέςεξπρές μόνο μέσωδωρεάν μεταβλητές. Το αντίστροφο του Gaussian αλγόριθμου λειτουργεί παραδοσιακά από κάτω προς τα πάνω. Από τη δεύτερη εξίσωση του συστήματος εκφράζουμε τη βασική μεταβλητή Χ 3:

Δείτε τώρα την πρώτη εξίσωση: . Πρώτα αντικαθιστούμε την έκφραση που βρέθηκε σε αυτήν:

Μένει να εκφράσουμε τη βασική μεταβλητή Χ 1 μέσω δωρεάν μεταβλητών Χ 2 και Χ 4:

Στο τέλος πήραμε αυτό που χρειαζόμασταν - Ολαβασικές μεταβλητές ( Χ 1 και Χ 3) εκφράζεται μόνο μέσωελεύθερες μεταβλητές ( Χ 2 και Χ 4):

Στην πραγματικότητα, η γενική λύση είναι έτοιμη:

Πώς να γράψετε σωστά τη γενική λύση; Πρώτα απ 'όλα, οι ελεύθερες μεταβλητές εγγράφονται στη γενική λύση "από μόνες τους" και αυστηρά στις θέσεις τους. ΣΕ σε αυτήν την περίπτωσηδωρεάν μεταβλητές Χ 2 και ΧΤο 4 πρέπει να γραφτεί στη δεύτερη και τέταρτη θέση:

Οι παραστάσεις που προκύπτουν για τις βασικές μεταβλητές και προφανώς πρέπει να γραφτεί στην πρώτη και τρίτη θέση:

Από τη γενική λύση του συστήματος μπορεί κανείς να βρει άπειρα πολλά ιδιωτικές λύσεις. Είναι πολύ απλό. Δωρεάν μεταβλητές Χ 2 και Χ 4 λέγονται έτσι γιατί μπορούν να δοθούν τυχόν τελικές τιμές. Οι πιο δημοφιλείς τιμές είναι μηδενικές, καθώς αυτή είναι η πιο εύκολη μερική λύση.

Αντικατάσταση ( Χ 2 = 0; Χ 4 = 0) στη γενική λύση, λαμβάνουμε μία από τις συγκεκριμένες λύσεις:

ή είναι μια συγκεκριμένη λύση που αντιστοιχεί σε ελεύθερες μεταβλητές με τιμές ( Χ 2 = 0; Χ 4 = 0).

Ένα άλλο γλυκό ζευγάρι είναι αυτά, ας αντικαταστήσουμε ( Χ 2 = 1 και Χ 4 = 1) στη γενική λύση:

, δηλαδή (-1; 1; 1; 1) - μια άλλη συγκεκριμένη λύση.

Είναι εύκολο να δούμε ότι το σύστημα των εξισώσεων έχει άπειρες λύσειςαφού μπορούμε να δώσουμε ελεύθερες μεταβλητές όποιοςνοήματα.

Καθεη συγκεκριμένη λύση πρέπει να ικανοποιεί στον καθέναεξίσωση του συστήματος. Αυτή είναι η βάση για έναν «γρήγορο» έλεγχο της ορθότητας της λύσης. Πάρτε, για παράδειγμα, τη συγκεκριμένη λύση (-1; 1; 1; 1) και αντικαταστήστε την στην αριστερή πλευρά κάθε εξίσωσης του αρχικού συστήματος:

Όλα πρέπει να ενωθούν. Και με οποιαδήποτε συγκεκριμένη λύση λαμβάνετε, όλα θα πρέπει επίσης να συμφωνούν.

Αυστηρά μιλώντας, ο έλεγχος μιας συγκεκριμένης λύσης είναι μερικές φορές παραπλανητικός, δηλ. κάποια συγκεκριμένη λύση μπορεί να ικανοποιεί κάθε εξίσωση του συστήματος, αλλά η ίδια η γενική λύση βρίσκεται στην πραγματικότητα λανθασμένα. Επομένως, πρώτα απ 'όλα, η επαλήθευση της γενικής λύσης είναι πιο εμπεριστατωμένη και αξιόπιστη.

Πώς να ελέγξετε τη γενική λύση που προκύπτει ?

Δεν είναι δύσκολο, αλλά απαιτεί μακροχρόνιες μετατροπές. Πρέπει να πάρουμε εκφράσεις βασικόςμεταβλητές, σε αυτή την περίπτωση και , και αντικαταστήστε τα στην αριστερή πλευρά κάθε εξίσωσης του συστήματος.

Στην αριστερή πλευρά της πρώτης εξίσωσης του συστήματος:

Λαμβάνεται η δεξιά πλευρά της αρχικής πρώτης εξίσωσης του συστήματος.

Στην αριστερή πλευρά της δεύτερης εξίσωσης του συστήματος:

Λαμβάνεται η δεξιά πλευρά της αρχικής δεύτερης εξίσωσης του συστήματος.

Και μετά - στην αριστερή πλευρά της τρίτης και τέταρτης εξίσωσης του συστήματος. Αυτός ο έλεγχος διαρκεί περισσότερο, αλλά εγγυάται 100% ορθότητα της συνολικής λύσης. Επιπλέον, ορισμένες εργασίες απαιτούν έλεγχο της γενικής λύσης.

Παράδειγμα 4:

Λύστε το σύστημα χρησιμοποιώντας τη μέθοδο Gauss. Βρείτε τη γενική λύση και δύο συγκεκριμένες. Ελέγξτε τη γενική λύση.

Αυτό είναι ένα παράδειγμα για να το λύσετε μόνοι σας. Εδώ, παρεμπιπτόντως, και πάλι ο αριθμός των εξισώσεων είναι μικρότερος από τον αριθμό των αγνώστων, πράγμα που σημαίνει ότι είναι αμέσως σαφές ότι το σύστημα είτε θα είναι ασυνεπές είτε θα έχει άπειρο αριθμό λύσεων.

Παράδειγμα 5:

Να λύσετε ένα σύστημα γραμμικών εξισώσεων. Εάν το σύστημα έχει άπειρες λύσεις, βρείτε δύο συγκεκριμένες λύσεις και ελέγξτε τη γενική λύση

Λύση:Ας γράψουμε τον εκτεταμένο πίνακα του συστήματος και, χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς, ας τον φέρουμε σε μια σταδιακή μορφή:

(1). Προσθέστε την πρώτη γραμμή στη δεύτερη γραμμή. Στην τρίτη γραμμή προσθέτουμε την πρώτη γραμμή πολλαπλασιαζόμενη επί 2. Στην τέταρτη γραμμή προσθέτουμε την πρώτη γραμμή πολλαπλασιαζόμενη επί 3.

(2). Στην τρίτη γραμμή προσθέτουμε τη δεύτερη γραμμή, πολλαπλασιαζόμενη επί (–5). Στην τέταρτη γραμμή προσθέτουμε τη δεύτερη γραμμή, πολλαπλασιαζόμενη επί (–7).

(3). Η τρίτη και η τέταρτη γραμμή είναι ίδιες, διαγράφουμε μία από αυτές. Αυτή είναι μια τέτοια ομορφιά:

Οι βασικές μεταβλητές κάθονται στα βήματα, επομένως - οι βασικές μεταβλητές.

Υπάρχει μόνο μία δωρεάν μεταβλητή που δεν έλαβε βήμα εδώ: .

(4). Αντίστροφη κίνηση. Ας εκφράσουμε τις βασικές μεταβλητές μέσω μιας ελεύθερης μεταβλητής:

Από την τρίτη εξίσωση:

Ας εξετάσουμε τη δεύτερη εξίσωση και ας αντικαταστήσουμε την έκφραση που βρέθηκε:

, , ,

Ας εξετάσουμε την πρώτη εξίσωση και ας αντικαταστήσουμε τις εκφράσεις που βρέθηκαν και σε αυτήν:

Έτσι, η γενική λύση με μία ελεύθερη μεταβλητή Χ 4:

Για άλλη μια φορά, πώς προέκυψε; Δωρεάν μεταβλητή ΧΤο 4 βρίσκεται μόνος του στην τέταρτη θέση που δικαιούται. Οι παραστάσεις που προκύπτουν για τις βασικές μεταβλητές , , είναι επίσης στη θέση τους.

Ας ελέγξουμε αμέσως τη γενική λύση.

Αντικαθιστούμε τις βασικές μεταβλητές , , στην αριστερή πλευρά κάθε εξίσωσης του συστήματος:

Λαμβάνονται οι αντίστοιχες δεξιές πλευρές των εξισώσεων, οπότε βρίσκεται η σωστή γενική λύση.

Τώρα από τη γενική λύση που βρέθηκε λαμβάνουμε δύο συγκεκριμένες λύσεις. Όλες οι μεταβλητές εκφράζονται εδώ μέσω μιας μοναδικής ελεύθερη μεταβλητή x 4 . Δεν χρειάζεται να μαζεύετε το μυαλό σας.

Αφήνω Χ 4 = 0 τότε – η πρώτη συγκεκριμένη λύση.

Αφήνω Χ 4 = 1 τότε – άλλη μια ιδιωτική λύση.

Απάντηση:Κοινή απόφαση: . Ιδιωτικές λύσεις:

Και .

Παράδειγμα 6:

Να βρείτε τη γενική λύση του συστήματος των γραμμικών εξισώσεων.

Έχουμε ήδη ελέγξει τη γενική λύση, η απάντηση μπορεί να είναι αξιόπιστη. Η λύση σας μπορεί να διαφέρει από τη λύση μας. Το κυριότερο είναι ότι οι γενικές αποφάσεις συμπίπτουν. Πολλοί άνθρωποι πιθανώς παρατήρησαν μια δυσάρεστη στιγμή στις λύσεις: πολύ συχνά, κατά την αντιστροφή της μεθόδου Gauss, έπρεπε να ασχοληθούμε με συνηθισμένα κλάσματα. Στην πράξη, αυτό συμβαίνει πράγματι οι περιπτώσεις όπου δεν υπάρχουν κλάσματα είναι πολύ λιγότερο συχνές. Να είστε προετοιμασμένοι ψυχικά και, κυρίως, τεχνικά.

Ας σταθούμε στα χαρακτηριστικά της λύσης που δεν βρέθηκαν στα λυμένα παραδείγματα. Η γενική λύση του συστήματος μπορεί μερικές φορές να περιλαμβάνει μια σταθερά (ή σταθερές).

Για παράδειγμα, μια γενική λύση: . Εδώ μία από τις βασικές μεταβλητές ισούται με σταθερός αριθμός: . Δεν υπάρχει τίποτα εξωτικό σε αυτό, συμβαίνει. Προφανώς, σε αυτή την περίπτωση, οποιαδήποτε συγκεκριμένη λύση θα περιέχει ένα πεντάρι στην πρώτη θέση.

Σπάνια, αλλά υπάρχουν συστήματα στα οποία ο αριθμός των εξισώσεων είναι μεγαλύτερος από τον αριθμό των μεταβλητών. Ωστόσο, η μέθοδος Gaussian λειτουργεί στις πιο σκληρές συνθήκες. Θα πρέπει να μειώσετε ήρεμα τον εκτεταμένο πίνακα του συστήματος σε μια σταδιακή μορφή χρησιμοποιώντας έναν τυπικό αλγόριθμο. Ένα τέτοιο σύστημα μπορεί να είναι ασυνεπές, μπορεί να έχει άπειρες λύσεις και, παραδόξως, μπορεί να έχει μία μόνο λύση.

Ας επαναλάβουμε τη συμβουλή μας - για να νιώθετε άνετα όταν λύνετε ένα σύστημα χρησιμοποιώντας τη μέθοδο Gaussian, θα πρέπει να είστε καλοί στην επίλυση τουλάχιστον δώδεκα συστημάτων.

Λύσεις και απαντήσεις:

Παράδειγμα 2:

Λύση:Ας γράψουμε τον εκτεταμένο πίνακα του συστήματος και, χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς, ας τον φέρουμε σε μια σταδιακή μορφή.

Οι στοιχειώδεις μετασχηματισμοί που πραγματοποιήθηκαν:

(1) Η πρώτη και η τρίτη γραμμή έχουν αλλάξει.

(2) Η πρώτη γραμμή προστέθηκε στη δεύτερη γραμμή, πολλαπλασιαζόμενη επί (–6). Η πρώτη γραμμή προστέθηκε στην τρίτη γραμμή, πολλαπλασιαζόμενη επί (–7).

(3) Η δεύτερη γραμμή προστέθηκε στην τρίτη γραμμή, πολλαπλασιαζόμενη επί (–1).

Ως αποτέλεσμα στοιχειωδών μετασχηματισμών, λαμβάνεται μια συμβολοσειρά της φόρμας, Οπου λ ≠ 0 .Αυτό σημαίνει ότι το σύστημα είναι ασυνεπές.Απάντηση: δεν υπάρχουν λύσεις.

Παράδειγμα 4:

Μετατροπές που πραγματοποιήθηκαν:

(1). Η πρώτη γραμμή, πολλαπλασιασμένη επί 2, προστέθηκε στη δεύτερη γραμμή Η πρώτη γραμμή, πολλαπλασιασμένη επί 3, προστέθηκε στην τρίτη γραμμή.

Δεν υπάρχει μονάδα για το δεύτερο βήμα , και ο μετασχηματισμός (2) στοχεύει στην απόκτησή του.

(2). Η τρίτη γραμμή προστέθηκε στη δεύτερη γραμμή, πολλαπλασιαζόμενη επί –3.

(3). Η δεύτερη και η τρίτη γραμμή άλλαξαν (μεταφέραμε το -1 που προέκυψε στο δεύτερο βήμα)

(4). Η τρίτη γραμμή προστέθηκε στη δεύτερη γραμμή, πολλαπλασιαζόμενη επί 3.

(5). Στις δύο πρώτες γραμμές άλλαξε το πρόσημο τους (πολλαπλασιάστηκε με –1), η τρίτη γραμμή διαιρέθηκε με το 14.

ΑΝΤΙΣΤΡΟΦΗ:

(1). Εδώ είναι οι βασικές μεταβλητές (οι οποίες βρίσκονται στα βήματα), και – δωρεάν μεταβλητές (που δεν πήραν βήμα).

(2). Ας εκφράσουμε τις βασικές μεταβλητές ως ελεύθερες μεταβλητές:

Από την τρίτη εξίσωση: .

(3). Θεωρήστε τη δεύτερη εξίσωση:, ιδιωτικές λύσεις:

Απάντηση: Κοινή απόφαση:

Μιγαδικοί αριθμοί

Σε αυτή την ενότητα θα παρουσιάσουμε την έννοια μιγαδικός αριθμός, σκεφτείτε αλγεβρικός, τριγωνομετρικήΚαι εκθετική μορφήμιγαδικός αριθμός. Θα μάθουμε επίσης πώς να εκτελούμε πράξεις με μιγαδικούς αριθμούς: πρόσθεση, αφαίρεση, πολλαπλασιασμό, διαίρεση, εκθετική εκτίμηση και εξαγωγή ρίζας.

Για να κατακτήσετε μιγαδικούς αριθμούς, δεν απαιτούνται ειδικές γνώσεις από ανώτερο μάθημα μαθηματικών και το υλικό είναι προσβάσιμο ακόμη και σε μαθητές σχολείου. Αρκεί να μπορείς να εκτελείς αλγεβρικές πράξεις με «συνηθισμένους» αριθμούς και να θυμάσαι τριγωνομετρία.

Αρχικά, ας θυμηθούμε τους «συνηθισμένους» Αριθμούς. Στα μαθηματικά λέγονται σύνολο πραγματικών αριθμώνκαι προσδιορίζονται με την επιστολή R,ή R (πυκνωμένο). Όλοι οι πραγματικοί αριθμοί βρίσκονται στη γνωστή αριθμητική γραμμή:

Η ομάδα των πραγματικών αριθμών είναι πολύ διαφορετική - υπάρχουν ακέραιοι αριθμοί, κλάσματα και παράλογοι αριθμοί. Σε αυτή την περίπτωση, κάθε σημείο στον άξονα αριθμών αντιστοιχεί απαραίτητα σε κάποιον πραγματικό αριθμό.