>

Λύση κλασματικών λογαρίθμων. Φυσικός λογάριθμος, συνάρτηση ln x

Ένα από τα στοιχεία της άλγεβρας αρχέγονου επιπέδου είναι ο λογάριθμος. Το όνομα προέρχεται από ελληνική γλώσσααπό τη λέξη «αριθμός» ή «δύναμη» και σημαίνει τη δύναμη στην οποία πρέπει να αυξηθεί ο αριθμός στη βάση για να βρεθεί ο τελικός αριθμός.

Τύποι λογαρίθμων

  • log a b – λογάριθμος του αριθμού b στη βάση του a (a > 0, a ≠ 1, b > 0);
  • log b – δεκαδικός λογάριθμος (λογάριθμος στη βάση 10, a = 10);
  • ln b – φυσικός λογάριθμος (λογάριθμος στη βάση e, a = e).

Πώς να λύσετε λογάριθμους;

Ο λογάριθμος του b στη βάση a είναι ένας εκθέτης που απαιτεί το b να αυξηθεί στη βάση a. Το αποτέλεσμα που προκύπτει προφέρεται ως εξής: «λογάριθμος του b στη βάση του a». Η λύση στα λογαριθμικά προβλήματα είναι ότι πρέπει να προσδιορίσετε τη δεδομένη ισχύ σε αριθμούς από τους καθορισμένους αριθμούς. Υπάρχουν ορισμένοι βασικοί κανόνες για τον προσδιορισμό ή την επίλυση του λογάριθμου, καθώς και τη μετατροπή της ίδιας της σημειογραφίας. Με τη χρήση τους γίνεται η λύση λογαριθμικές εξισώσεις, βρίσκονται οι παράγωγοι, επιλύονται ολοκληρώματα και εκτελούνται πολλές άλλες πράξεις. Βασικά, η λύση στον ίδιο τον λογάριθμο είναι η απλοποιημένη σημειογραφία του. Παρακάτω είναι οι βασικοί τύποι και ιδιότητες:

Για οποιαδήποτε ? a > 0; a ≠ 1 και για οποιοδήποτε x ; y > 0.

  • a log a b = b – βασική λογαριθμική ταυτότητα
  • καταγράψτε a 1 = 0
  • loga a = 1
  • log a (x y) = log a x + log a y
  • log a x/ y = log a x – log a y
  • log a 1/x = -log a x
  • log a x p = p log a x
  • log a k x = 1/k log a x, για k ≠ 0
  • log a x = log a c x c
  • log a x = log b x/ log b a – τύπος για μετάβαση σε νέα βάση
  • log a x = 1/log x a


Πώς να λύσετε λογάριθμους - οδηγίες βήμα προς βήμα για την επίλυση

  • Αρχικά, γράψτε την απαιτούμενη εξίσωση.

Παρακαλώ σημειώστε: εάν ο βασικός λογάριθμος είναι 10, τότε η καταχώρηση συντομεύεται, καταλήγοντας σε δεκαδικό λογάριθμο. Αν αξίζει φυσικός αριθμόςε, στη συνέχεια το γράφουμε, ανάγοντάς το στον φυσικό λογάριθμο. Αυτό σημαίνει ότι το αποτέλεσμα όλων των λογαρίθμων είναι η ισχύς στην οποία αυξάνεται ο βασικός αριθμός για να ληφθεί ο αριθμός b.


Άμεσα, η λύση βρίσκεται στον υπολογισμό αυτού του βαθμού. Πριν λύσετε μια παράσταση με λογάριθμο, πρέπει να απλοποιηθεί σύμφωνα με τον κανόνα, δηλαδή χρησιμοποιώντας τύπους. Μπορείτε να βρείτε τις κύριες ταυτότητες ανατρέχοντας λίγο πίσω στο άρθρο.

Πρόσθεση και αφαίρεση λογαρίθμων με δύο διαφορετικούς αριθμούς, αλλά με τις ίδιες βάσεις, αντικαταστήστε με έναν λογάριθμο με το γινόμενο ή τη διαίρεση των αριθμών b και c, αντίστοιχα. Σε αυτήν την περίπτωση, μπορείτε να εφαρμόσετε τον τύπο για τη μετάβαση σε άλλη βάση (βλ. παραπάνω).

Εάν χρησιμοποιείτε εκφράσεις για να απλοποιήσετε έναν λογάριθμο, υπάρχουν ορισμένοι περιορισμοί που πρέπει να λάβετε υπόψη. Και αυτό είναι: η βάση του λογάριθμου α είναι μόνο ένας θετικός αριθμός, αλλά όχι ίσος με ένα. Ο αριθμός b, όπως και το a, πρέπει να είναι μεγαλύτερος από το μηδέν.

Υπάρχουν περιπτώσεις όπου, απλοποιώντας μια έκφραση, δεν θα μπορείτε να υπολογίσετε τον λογάριθμο αριθμητικά. Συμβαίνει ότι μια τέτοια έκφραση δεν έχει νόημα, επειδή πολλές δυνάμεις είναι παράλογοι αριθμοί. Υπό αυτήν την προϋπόθεση, αφήστε την ισχύ του αριθμού ως λογάριθμο.



κύριες ιδιότητες.

  1. logax + logay = loga(x y);
  2. logax − logay = λογάριθμος (x: y).

πανομοιότυπους λόγους

Log6 4 + log6 9.

Τώρα ας περιπλέκουμε λίγο το έργο.

Παραδείγματα επίλυσης λογαρίθμων

Τι γίνεται αν η βάση ή το όρισμα ενός λογαρίθμου είναι δύναμη; Τότε ο εκθέτης αυτού του βαθμού μπορεί να αφαιρεθεί από το πρόσημο του λογαρίθμου σύμφωνα με τους ακόλουθους κανόνες:

Φυσικά, όλοι αυτοί οι κανόνες έχουν νόημα αν παρατηρηθεί το ODZ του λογαρίθμου: a > 0, a ≠ 1, x >

Εργο. Βρείτε το νόημα της έκφρασης:

Μετάβαση σε νέα βάση

Ας δοθεί ο λογάριθμος λογάριθμος. Τότε για οποιονδήποτε αριθμό c τέτοιο ώστε c > 0 και c ≠ 1, η ισότητα είναι αληθής:

Εργο. Βρείτε το νόημα της έκφρασης:

Δείτε επίσης:


Βασικές ιδιότητες του λογάριθμου

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.



Ο εκθέτης είναι 2,718281828…. Για να θυμάστε τον εκθέτη, μπορείτε να μελετήσετε τον κανόνα: ο εκθέτης είναι ίσος με 2,7 και διπλάσιο από το έτος γέννησης του Λέοντος Νικολάεβιτς Τολστόι.

Βασικές ιδιότητες των λογαρίθμων

Γνωρίζοντας αυτόν τον κανόνα θα γνωρίζετε και ακριβής αξίαεκθέτες και την ημερομηνία γέννησης του Λέοντος Τολστόι.


Παραδείγματα για λογάριθμους

Λογαρίθμες εκφράσεις

Παράδειγμα 1.
ΕΝΑ). x=10ac^2 (a>0,c>0).

Χρησιμοποιώντας ιδιότητες 3.5 υπολογίζουμε

2.

3.

4. Οπου .



Παράδειγμα 2. Βρείτε το x αν


Παράδειγμα 3. Έστω η τιμή των λογαρίθμων

Υπολογίστε το log(x) αν




Βασικές ιδιότητες των λογαρίθμων

Οι λογάριθμοι, όπως κάθε αριθμός, μπορούν να προστεθούν, να αφαιρεθούν και να μετασχηματιστούν με κάθε τρόπο. Αλλά επειδή οι λογάριθμοι δεν είναι ακριβώς συνηθισμένοι αριθμοί, υπάρχουν κανόνες εδώ, οι οποίοι καλούνται κύριες ιδιότητες.

Πρέπει οπωσδήποτε να γνωρίζετε αυτούς τους κανόνες - κανένα σοβαρό λογαριθμικό πρόβλημα δεν μπορεί να λυθεί χωρίς αυτούς. Επιπλέον, υπάρχουν πολύ λίγα από αυτά - μπορείτε να μάθετε τα πάντα σε μια μέρα. Ας ξεκινήσουμε λοιπόν.

Πρόσθεση και αφαίρεση λογαρίθμων

Θεωρήστε δύο λογάριθμους με τις ίδιες βάσεις: λογάξ και λογάριθμο. Στη συνέχεια μπορούν να προστεθούν και να αφαιρεθούν και:

  1. logax + logay = loga(x y);
  2. logax − logay = λογάριθμος (x: y).

Άρα, το άθροισμα των λογαρίθμων είναι ίσο με τον λογάριθμο του γινομένου και η διαφορά είναι ίση με τον λογάριθμο του πηλίκου. Παρακαλώ σημειώστε: το βασικό σημείο εδώ είναι πανομοιότυπους λόγους. Εάν οι λόγοι είναι διαφορετικοί, αυτοί οι κανόνες δεν λειτουργούν!

Αυτοί οι τύποι θα σας βοηθήσουν να υπολογίσετε λογαριθμική έκφρασηακόμη και όταν τα επιμέρους μέρη του δεν υπολογίζονται (δείτε το μάθημα «Τι είναι λογάριθμος»). Ρίξτε μια ματιά στα παραδείγματα και δείτε:

Επειδή οι λογάριθμοι έχουν τις ίδιες βάσεις, χρησιμοποιούμε τον τύπο αθροίσματος:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Εργο. Βρείτε την τιμή της παράστασης: log2 48 − log2 3.

Οι βάσεις είναι ίδιες, χρησιμοποιούμε τον τύπο διαφοράς:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.

Εργο. Βρείτε την τιμή της παράστασης: log3 135 − log3 5.

Και πάλι οι βάσεις είναι ίδιες, οπότε έχουμε:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Όπως μπορείτε να δείτε, οι αρχικές εκφράσεις αποτελούνται από «κακούς» λογάριθμους, οι οποίοι δεν υπολογίζονται χωριστά. Όμως μετά τους μετασχηματισμούς προκύπτουν εντελώς κανονικοί αριθμοί. Πολλοί βασίζονται σε αυτό το γεγονός δοκιμαστικά χαρτιά. Ναι, οι εκφράσεις που μοιάζουν με τεστ προσφέρονται με κάθε σοβαρότητα (μερικές φορές χωρίς σχεδόν καμία αλλαγή) στην Εξέταση Ενιαίου Κράτους.

Εξαγωγή του εκθέτη από τον λογάριθμο

Είναι εύκολο να δει κανείς ότι ο τελευταίος κανόνας ακολουθεί τους δύο πρώτους. Αλλά είναι καλύτερα να το θυμάστε ούτως ή άλλως - σε ορισμένες περιπτώσεις θα μειώσει σημαντικά τον όγκο των υπολογισμών.

Φυσικά, όλοι αυτοί οι κανόνες έχουν νόημα αν παρατηρηθεί το ODZ του λογαρίθμου: a > 0, a ≠ 1, x > 0. Και κάτι ακόμα: μάθετε να εφαρμόζετε όλους τους τύπους όχι μόνο από αριστερά προς τα δεξιά, αλλά και αντίστροφα , δηλ. Μπορείτε να εισάγετε τους αριθμούς πριν από το σύμβολο του λογάριθμου στον ίδιο τον λογάριθμο. Αυτό είναι που απαιτείται συχνότερα.

Εργο. Βρείτε την τιμή της παράστασης: log7 496.

Ας απαλλαγούμε από το βαθμό στο όρισμα χρησιμοποιώντας τον πρώτο τύπο:
log7 496 = 6 log7 49 = 6 2 = 12

Εργο. Βρείτε το νόημα της έκφρασης:

Σημειώστε ότι ο παρονομαστής περιέχει έναν λογάριθμο, η βάση και το όρισμα του οποίου είναι ακριβείς δυνάμεις: 16 = 24; 49 = 72. Έχουμε:

Νομίζω ότι το τελευταίο παράδειγμα απαιτεί κάποια διευκρίνιση. Πού πήγαν οι λογάριθμοι; Μέχρι το πολύ τελευταία στιγμήδουλεύουμε μόνο με τον παρονομαστή.

Τύποι λογαρίθμων. Παραδείγματα λογαρίθμων λύσεων.

Παρουσιάσαμε τη βάση και το όρισμα του λογάριθμου που στέκεται εκεί με τη μορφή δυνάμεων και βγάλαμε τους εκθέτες - πήραμε ένα κλάσμα "τριώροφο".

Τώρα ας δούμε το κύριο κλάσμα. Ο αριθμητής και ο παρονομαστής περιέχουν τον ίδιο αριθμό: log2 7. Επειδή log2 7 ≠ 0, μπορούμε να μειώσουμε το κλάσμα - τα 2/4 θα παραμείνουν στον παρονομαστή. Σύμφωνα με τους κανόνες της αριθμητικής, τα τέσσερα μπορούν να μεταφερθούν στον αριθμητή, πράγμα που έγινε. Το αποτέλεσμα ήταν η απάντηση: 2.

Μετάβαση σε νέα βάση

Μιλώντας για τους κανόνες πρόσθεσης και αφαίρεσης λογαρίθμων, τόνισα συγκεκριμένα ότι λειτουργούν μόνο με τις ίδιες βάσεις. Κι αν οι λόγοι είναι διαφορετικοί; Τι γίνεται αν δεν είναι ακριβείς δυνάμεις του ίδιου αριθμού;

Οι φόρμουλες για τη μετάβαση σε ένα νέο θεμέλιο έρχονται στη διάσωση. Ας τα διατυπώσουμε με τη μορφή ενός θεωρήματος:

Ας δοθεί ο λογάριθμος λογάριθμος. Τότε για οποιονδήποτε αριθμό c τέτοιο ώστε c > 0 και c ≠ 1, η ισότητα είναι αληθής:

Συγκεκριμένα, αν θέσουμε c = x, παίρνουμε:

Από τον δεύτερο τύπο προκύπτει ότι η βάση και το όρισμα του λογάριθμου μπορούν να αντικατασταθούν, αλλά σε αυτήν την περίπτωση ολόκληρη η έκφραση "αναποδογυρίζεται", δηλ. ο λογάριθμος εμφανίζεται στον παρονομαστή.

Αυτοί οι τύποι σπάνια βρίσκονται σε συμβατικές αριθμητικές εκφράσεις. Είναι δυνατό να αξιολογήσουμε πόσο βολικές είναι μόνο όταν λύνουμε λογαριθμικές εξισώσεις και ανισώσεις.

Ωστόσο, υπάρχουν προβλήματα που δεν μπορούν να λυθούν καθόλου παρά μόνο με τη μετάβαση σε ένα νέο θεμέλιο. Ας δούμε μερικά από αυτά:

Εργο. Βρείτε την τιμή της παράστασης: log5 16 log2 25.

Σημειώστε ότι τα ορίσματα και των δύο λογαρίθμων περιέχουν ακριβείς δυνάμεις. Ας βγάλουμε τους δείκτες: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

Τώρα ας «αντιστρέψουμε» τον δεύτερο λογάριθμο:

Δεδομένου ότι το γινόμενο δεν αλλάζει κατά την αναδιάταξη των παραγόντων, πολλαπλασιάσαμε ήρεμα τέσσερα και δύο και στη συνέχεια ασχοληθήκαμε με τους λογάριθμους.

Εργο. Βρείτε την τιμή της παράστασης: log9 100 lg 3.

Η βάση και το όρισμα του πρώτου λογάριθμου είναι ακριβείς δυνάμεις. Ας το γράψουμε αυτό και ας απαλλαγούμε από τους δείκτες:

Τώρα ας απαλλαγούμε από τον δεκαδικό λογάριθμο μεταβαίνοντας σε μια νέα βάση:

Βασική λογαριθμική ταυτότητα

Συχνά στη διαδικασία επίλυσης είναι απαραίτητο να αναπαραστήσουμε έναν αριθμό ως λογάριθμο σε μια δεδομένη βάση. Σε αυτήν την περίπτωση, οι παρακάτω τύποι θα μας βοηθήσουν:

Στην πρώτη περίπτωση, ο αριθμός n γίνεται ο εκθέτης στο όρισμα. Ο αριθμός n μπορεί να είναι απολύτως οτιδήποτε, γιατί είναι απλώς μια λογαριθμική τιμή.

Ο δεύτερος τύπος είναι στην πραγματικότητα ένας παραφρασμένος ορισμός. Έτσι λέγεται: .

Στην πραγματικότητα, τι συμβαίνει εάν ο αριθμός b αυξηθεί σε τέτοια δύναμη ώστε ο αριθμός b σε αυτή τη δύναμη να δώσει τον αριθμό a; Αυτό είναι σωστό: το αποτέλεσμα είναι ο ίδιος αριθμός α. Διαβάστε ξανά προσεκτικά αυτήν την παράγραφο - πολλοί άνθρωποι κολλάνε σε αυτήν.

Όπως οι τύποι για τη μετάβαση σε μια νέα βάση, η βασική λογαριθμική ταυτότητα είναι μερικές φορές η μόνη δυνατή λύση.

Εργο. Βρείτε το νόημα της έκφρασης:

Σημειώστε ότι log25 64 = log5 8 - απλά πήρε το τετράγωνο από τη βάση και το όρισμα του λογαρίθμου. Λαμβάνοντας υπόψη τους κανόνες για τον πολλαπλασιασμό των δυνάμεων με την ίδια βάση, παίρνουμε:

Αν κάποιος δεν ξέρει, αυτή ήταν μια πραγματική εργασία από την Ενιαία Κρατική Εξέταση :)

Λογαριθμική μονάδα και λογαριθμικό μηδέν

Εν κατακλείδι, θα δώσω δύο ταυτότητες που δύσκολα μπορούν να ονομαστούν ιδιότητες - μάλλον είναι συνέπειες του ορισμού του λογαρίθμου. Εμφανίζονται συνεχώς σε προβλήματα και, παραδόξως, δημιουργούν προβλήματα ακόμη και σε «προχωρημένους» μαθητές.

  1. λογάα = 1 είναι. Θυμηθείτε μια για πάντα: ο λογάριθμος σε οποιαδήποτε βάση α αυτής της ίδιας της βάσης είναι ίσος με ένα.
  2. λογότυπο 1 = 0 είναι. Η βάση a μπορεί να είναι οτιδήποτε, αλλά αν το όρισμα περιέχει ένα, ο λογάριθμος είναι ίσος με μηδέν! Επειδή το a0 = 1 είναι άμεση συνέπεια του ορισμού.

Αυτά είναι όλα τα ακίνητα. Φροντίστε να εξασκηθείτε στην εφαρμογή τους! Κατεβάστε το cheat sheet στην αρχή του μαθήματος, εκτυπώστε το και λύστε τα προβλήματα.

Δείτε επίσης:

Ο λογάριθμος του b για τη βάση του a δηλώνει την παράσταση. Για να υπολογίσετε τον λογάριθμο σημαίνει να βρείτε μια ισχύ x () στην οποία η ισότητα ικανοποιείται

Βασικές ιδιότητες του λογάριθμου

Είναι απαραίτητο να γνωρίζουμε τις παραπάνω ιδιότητες, αφού όλα σχεδόν τα προβλήματα και τα παραδείγματα που σχετίζονται με τους λογάριθμους επιλύονται με βάση τους. Οι υπόλοιπες εξωτικές ιδιότητες μπορούν να προκύψουν μέσω μαθηματικών χειρισμών με αυτούς τους τύπους

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

Κατά τον υπολογισμό του τύπου για το άθροισμα και τη διαφορά των λογαρίθμων (3.4) συναντάτε αρκετά συχνά. Τα υπόλοιπα είναι κάπως περίπλοκα, αλλά σε μια σειρά εργασιών είναι απαραίτητα για την απλοποίηση σύνθετων εκφράσεων και τον υπολογισμό των τιμών τους.

Συνήθεις περιπτώσεις λογαρίθμων

Μερικοί από τους πιο συνηθισμένους λογάριθμους είναι εκείνοι στους οποίους η βάση είναι ίση με δέκα, εκθετική ή δύο.
Ο λογάριθμος στη βάση δέκα ονομάζεται συνήθως δεκαδικός λογάριθμος και συμβολίζεται απλώς με lg(x).

Από την ηχογράφηση φαίνεται ξεκάθαρα ότι στην ηχογράφηση δεν γράφονται τα βασικά. Για παράδειγμα

Φυσικός λογάριθμοςείναι ένας λογάριθμος με βάση έναν εκθέτη (συμβολίζεται με ln(x)).

Ο εκθέτης είναι 2,718281828…. Για να θυμάστε τον εκθέτη, μπορείτε να μελετήσετε τον κανόνα: ο εκθέτης είναι ίσος με 2,7 και δύο φορές το έτος γέννησης του Λέοντος Νικολάεβιτς Τολστόι. Γνωρίζοντας αυτόν τον κανόνα, θα γνωρίζετε τόσο την ακριβή τιμή του εκθέτη όσο και την ημερομηνία γέννησης του Λέοντος Τολστόι.

Και ένας άλλος σημαντικός λογάριθμος για τη βάση δύο συμβολίζεται με

Η παράγωγος του λογάριθμου μιας συνάρτησης είναι ίση με ένα διαιρούμενο με τη μεταβλητή

Ο ολοκληρωτικός ή αντιπαράγωγος λογάριθμος καθορίζεται από τη σχέση

Το δεδομένο υλικό είναι αρκετό για να λύσετε μια ευρεία κατηγορία προβλημάτων που σχετίζονται με λογάριθμους και λογάριθμους. Για να σας βοηθήσω να κατανοήσετε το υλικό, θα δώσω μόνο μερικά κοινά παραδείγματα από σχολικό πρόγραμμα σπουδώνκαι πανεπιστήμια.

Παραδείγματα για λογάριθμους

Λογαρίθμες εκφράσεις

Παράδειγμα 1.
ΕΝΑ). x=10ac^2 (a>0,c>0).

Χρησιμοποιώντας ιδιότητες 3.5 υπολογίζουμε

2.
Με την ιδιότητα διαφοράς λογαρίθμων έχουμε

3.
Χρησιμοποιώντας ιδιότητες 3.5 βρίσκουμε

4. Οπου .

Μια φαινομενικά πολύπλοκη έκφραση απλοποιείται για να σχηματιστεί χρησιμοποιώντας έναν αριθμό κανόνων

Εύρεση λογαριθμικών τιμών

Παράδειγμα 2. Βρείτε το x αν

Λύση. Για τον υπολογισμό, εφαρμόζουμε στον τελευταίο όρο 5 και 13 ιδιότητες

Το βάζουμε σε δίσκο και θρηνούμε

Εφόσον οι βάσεις είναι ίσες, εξισώνουμε τις εκφράσεις

Λογάριθμοι. Πρώτο επίπεδο.

Ας δοθεί η τιμή των λογαρίθμων

Υπολογίστε το log(x) αν

Λύση: Ας πάρουμε έναν λογάριθμο της μεταβλητής για να γράψουμε τον λογάριθμο μέσω του αθροίσματος των όρων της


Αυτή είναι μόνο η αρχή της γνωριμίας μας με τους λογάριθμους και τις ιδιότητές τους. Εξασκηθείτε στους υπολογισμούς, εμπλουτίστε τις πρακτικές σας δεξιότητες - σύντομα θα χρειαστείτε τις γνώσεις που αποκτάτε για να λύσετε λογαριθμικές εξισώσεις. Έχοντας μελετήσει τις βασικές μεθόδους για την επίλυση τέτοιων εξισώσεων, θα επεκτείνουμε τις γνώσεις σας σε ένα άλλο εξίσου σημαντικό θέμα - τις λογαριθμικές ανισότητες...

Βασικές ιδιότητες των λογαρίθμων

Οι λογάριθμοι, όπως κάθε αριθμός, μπορούν να προστεθούν, να αφαιρεθούν και να μετασχηματιστούν με κάθε τρόπο. Αλλά επειδή οι λογάριθμοι δεν είναι ακριβώς συνηθισμένοι αριθμοί, υπάρχουν κανόνες εδώ, οι οποίοι καλούνται κύριες ιδιότητες.

Πρέπει οπωσδήποτε να γνωρίζετε αυτούς τους κανόνες - κανένα σοβαρό λογαριθμικό πρόβλημα δεν μπορεί να λυθεί χωρίς αυτούς. Επιπλέον, υπάρχουν πολύ λίγα από αυτά - μπορείτε να μάθετε τα πάντα σε μια μέρα. Ας ξεκινήσουμε λοιπόν.

Πρόσθεση και αφαίρεση λογαρίθμων

Θεωρήστε δύο λογάριθμους με τις ίδιες βάσεις: λογάξ και λογάριθμο. Στη συνέχεια μπορούν να προστεθούν και να αφαιρεθούν και:

  1. logax + logay = loga(x y);
  2. logax − logay = λογάριθμος (x: y).

Άρα, το άθροισμα των λογαρίθμων είναι ίσο με τον λογάριθμο του γινομένου και η διαφορά είναι ίση με τον λογάριθμο του πηλίκου. Παρακαλώ σημειώστε: το βασικό σημείο εδώ είναι πανομοιότυπους λόγους. Εάν οι λόγοι είναι διαφορετικοί, αυτοί οι κανόνες δεν λειτουργούν!

Αυτοί οι τύποι θα σας βοηθήσουν να υπολογίσετε μια λογαριθμική παράσταση ακόμα και όταν δεν λαμβάνονται υπόψη τα επιμέρους μέρη της (δείτε το μάθημα «Τι είναι ο λογάριθμος»). Ρίξτε μια ματιά στα παραδείγματα και δείτε:

Εργο. Βρείτε την τιμή της παράστασης: log6 4 + log6 9.

Επειδή οι λογάριθμοι έχουν τις ίδιες βάσεις, χρησιμοποιούμε τον τύπο αθροίσματος:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Εργο. Βρείτε την τιμή της παράστασης: log2 48 − log2 3.

Οι βάσεις είναι ίδιες, χρησιμοποιούμε τον τύπο διαφοράς:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.

Εργο. Βρείτε την τιμή της παράστασης: log3 135 − log3 5.

Και πάλι οι βάσεις είναι ίδιες, οπότε έχουμε:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Όπως μπορείτε να δείτε, οι αρχικές εκφράσεις αποτελούνται από «κακούς» λογάριθμους, οι οποίοι δεν υπολογίζονται χωριστά. Όμως μετά τους μετασχηματισμούς προκύπτουν εντελώς κανονικοί αριθμοί. Πολλά τεστ βασίζονται σε αυτό το γεγονός. Ναι, οι εκφράσεις που μοιάζουν με τεστ προσφέρονται με κάθε σοβαρότητα (μερικές φορές χωρίς σχεδόν καμία αλλαγή) στην Εξέταση Ενιαίου Κράτους.

Εξαγωγή του εκθέτη από τον λογάριθμο

Τώρα ας περιπλέκουμε λίγο το έργο. Τι γίνεται αν η βάση ή το όρισμα ενός λογαρίθμου είναι δύναμη; Τότε ο εκθέτης αυτού του βαθμού μπορεί να αφαιρεθεί από το πρόσημο του λογαρίθμου σύμφωνα με τους ακόλουθους κανόνες:

Είναι εύκολο να δει κανείς ότι ο τελευταίος κανόνας ακολουθεί τους δύο πρώτους. Αλλά είναι καλύτερα να το θυμάστε ούτως ή άλλως - σε ορισμένες περιπτώσεις θα μειώσει σημαντικά τον όγκο των υπολογισμών.

Φυσικά, όλοι αυτοί οι κανόνες έχουν νόημα αν παρατηρηθεί το ODZ του λογαρίθμου: a > 0, a ≠ 1, x > 0. Και κάτι ακόμα: μάθετε να εφαρμόζετε όλους τους τύπους όχι μόνο από αριστερά προς τα δεξιά, αλλά και αντίστροφα , δηλ. Μπορείτε να εισάγετε τους αριθμούς πριν από το σύμβολο του λογάριθμου στον ίδιο τον λογάριθμο.

Πώς να λύσετε λογάριθμους

Αυτό είναι που απαιτείται συχνότερα.

Εργο. Βρείτε την τιμή της παράστασης: log7 496.

Ας απαλλαγούμε από το βαθμό στο όρισμα χρησιμοποιώντας τον πρώτο τύπο:
log7 496 = 6 log7 49 = 6 2 = 12

Εργο. Βρείτε το νόημα της έκφρασης:

Σημειώστε ότι ο παρονομαστής περιέχει έναν λογάριθμο, η βάση και το όρισμα του οποίου είναι ακριβείς δυνάμεις: 16 = 24; 49 = 72. Έχουμε:

Νομίζω ότι το τελευταίο παράδειγμα απαιτεί κάποια διευκρίνιση. Πού πήγαν οι λογάριθμοι; Μέχρι την τελευταία στιγμή δουλεύουμε μόνο με τον παρονομαστή. Παρουσιάσαμε τη βάση και το όρισμα του λογάριθμου που στέκεται εκεί με τη μορφή δυνάμεων και βγάλαμε τους εκθέτες - πήραμε ένα κλάσμα "τριώροφο".

Τώρα ας δούμε το κύριο κλάσμα. Ο αριθμητής και ο παρονομαστής περιέχουν τον ίδιο αριθμό: log2 7. Επειδή log2 7 ≠ 0, μπορούμε να μειώσουμε το κλάσμα - τα 2/4 θα παραμείνουν στον παρονομαστή. Σύμφωνα με τους κανόνες της αριθμητικής, τα τέσσερα μπορούν να μεταφερθούν στον αριθμητή, πράγμα που έγινε. Το αποτέλεσμα ήταν η απάντηση: 2.

Μετάβαση σε νέα βάση

Μιλώντας για τους κανόνες πρόσθεσης και αφαίρεσης λογαρίθμων, τόνισα συγκεκριμένα ότι λειτουργούν μόνο με τις ίδιες βάσεις. Κι αν οι λόγοι είναι διαφορετικοί; Τι γίνεται αν δεν είναι ακριβείς δυνάμεις του ίδιου αριθμού;

Οι φόρμουλες για τη μετάβαση σε ένα νέο θεμέλιο έρχονται στη διάσωση. Ας τα διατυπώσουμε με τη μορφή ενός θεωρήματος:

Ας δοθεί ο λογάριθμος λογάριθμος. Τότε για οποιονδήποτε αριθμό c τέτοιο ώστε c > 0 και c ≠ 1, η ισότητα είναι αληθής:

Συγκεκριμένα, αν θέσουμε c = x, παίρνουμε:

Από τον δεύτερο τύπο προκύπτει ότι η βάση και το όρισμα του λογάριθμου μπορούν να αντικατασταθούν, αλλά σε αυτήν την περίπτωση ολόκληρη η έκφραση "αναποδογυρίζεται", δηλ. ο λογάριθμος εμφανίζεται στον παρονομαστή.

Αυτοί οι τύποι βρίσκονται σπάνια σε συνηθισμένες αριθμητικές εκφράσεις. Είναι δυνατό να αξιολογήσουμε πόσο βολικές είναι μόνο όταν λύνουμε λογαριθμικές εξισώσεις και ανισώσεις.

Ωστόσο, υπάρχουν προβλήματα που δεν μπορούν να λυθούν καθόλου παρά μόνο με τη μετάβαση σε ένα νέο θεμέλιο. Ας δούμε μερικά από αυτά:

Εργο. Βρείτε την τιμή της παράστασης: log5 16 log2 25.

Σημειώστε ότι τα ορίσματα και των δύο λογαρίθμων περιέχουν ακριβείς δυνάμεις. Ας βγάλουμε τους δείκτες: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

Τώρα ας «αντιστρέψουμε» τον δεύτερο λογάριθμο:

Δεδομένου ότι το γινόμενο δεν αλλάζει κατά την αναδιάταξη των παραγόντων, πολλαπλασιάσαμε ήρεμα τέσσερα και δύο και στη συνέχεια ασχοληθήκαμε με τους λογάριθμους.

Εργο. Βρείτε την τιμή της παράστασης: log9 100 lg 3.

Η βάση και το όρισμα του πρώτου λογάριθμου είναι ακριβείς δυνάμεις. Ας το γράψουμε αυτό και ας απαλλαγούμε από τους δείκτες:

Τώρα ας απαλλαγούμε από τον δεκαδικό λογάριθμο μεταβαίνοντας σε μια νέα βάση:

Βασική λογαριθμική ταυτότητα

Συχνά στη διαδικασία επίλυσης είναι απαραίτητο να αναπαραστήσουμε έναν αριθμό ως λογάριθμο σε μια δεδομένη βάση. Σε αυτήν την περίπτωση, οι παρακάτω τύποι θα μας βοηθήσουν:

Στην πρώτη περίπτωση, ο αριθμός n γίνεται ο εκθέτης στο όρισμα. Ο αριθμός n μπορεί να είναι απολύτως οτιδήποτε, γιατί είναι απλώς μια λογαριθμική τιμή.

Ο δεύτερος τύπος είναι στην πραγματικότητα ένας παραφρασμένος ορισμός. Έτσι λέγεται: .

Στην πραγματικότητα, τι συμβαίνει εάν ο αριθμός b αυξηθεί σε τέτοια δύναμη ώστε ο αριθμός b σε αυτή τη δύναμη να δώσει τον αριθμό a; Αυτό είναι σωστό: το αποτέλεσμα είναι ο ίδιος αριθμός α. Διαβάστε ξανά προσεκτικά αυτήν την παράγραφο - πολλοί άνθρωποι κολλάνε σε αυτήν.

Όπως οι τύποι για τη μετάβαση σε μια νέα βάση, η βασική λογαριθμική ταυτότητα είναι μερικές φορές η μόνη δυνατή λύση.

Εργο. Βρείτε το νόημα της έκφρασης:

Σημειώστε ότι log25 64 = log5 8 - απλά πήρε το τετράγωνο από τη βάση και το όρισμα του λογαρίθμου. Λαμβάνοντας υπόψη τους κανόνες για τον πολλαπλασιασμό των δυνάμεων με την ίδια βάση, παίρνουμε:

Αν κάποιος δεν ξέρει, αυτή ήταν μια πραγματική εργασία από την Ενιαία Κρατική Εξέταση :)

Λογαριθμική μονάδα και λογαριθμικό μηδέν

Εν κατακλείδι, θα δώσω δύο ταυτότητες που δύσκολα μπορούν να ονομαστούν ιδιότητες - μάλλον είναι συνέπειες του ορισμού του λογαρίθμου. Εμφανίζονται συνεχώς σε προβλήματα και, παραδόξως, δημιουργούν προβλήματα ακόμη και σε «προχωρημένους» μαθητές.

  1. λογάα = 1 είναι. Θυμηθείτε μια για πάντα: ο λογάριθμος σε οποιαδήποτε βάση α αυτής της ίδιας της βάσης είναι ίσος με ένα.
  2. λογότυπο 1 = 0 είναι. Η βάση a μπορεί να είναι οτιδήποτε, αλλά αν το όρισμα περιέχει ένα, ο λογάριθμος είναι ίσος με μηδέν! Επειδή το a0 = 1 είναι άμεση συνέπεια του ορισμού.

Αυτά είναι όλα τα ακίνητα. Φροντίστε να εξασκηθείτε στην εφαρμογή τους! Κατεβάστε το cheat sheet στην αρχή του μαθήματος, εκτυπώστε το και λύστε τα προβλήματα.

Οι βασικές ιδιότητες του φυσικού λογάριθμου, γράφημα, πεδίο ορισμού, σύνολο τιμών, βασικοί τύποι, παράγωγος, ολοκλήρωμα, επέκταση σε σειρά ισχύοςκαι αναπαράσταση της συνάρτησης ln x με χρήση μιγαδικών αριθμών.

Ορισμός

Φυσικός λογάριθμοςείναι η συνάρτηση y = Στο x, το αντίστροφο της εκθετικής, x = e y, και είναι ο λογάριθμος στη βάση του αριθμού e: ln x = log e x.

Ο φυσικός λογάριθμος χρησιμοποιείται ευρέως στα μαθηματικά επειδή η παράγωγός του έχει την απλούστερη μορφή: (ln x)′ = 1/ x.

Με βάση ορισμοί, η βάση του φυσικού λογάριθμου είναι ο αριθμός μι:
e ≅ 2,718281828459045...;
.

Γράφημα της συνάρτησης y = Στο x.

Γράφημα φυσικού λογάριθμου (συναρτήσεις y = Στο x) προκύπτει από το εκθετικό γράφημα εικόνα καθρέφτησε σχέση με την ευθεία y = x.

Ο φυσικός λογάριθμος ορίζεται για θετικές τιμές της μεταβλητής x.

Αυξάνεται μονότονα στο πεδίο ορισμού του. 0 Στο x →

το όριο του φυσικού λογάριθμου είναι μείον το άπειρο (-∞). Ως x → + ∞, το όριο του φυσικού λογάριθμου είναι συν άπειρο (+ ∞). Για μεγάλο x, ο λογάριθμος αυξάνεται αρκετά αργά. Οποιοςλειτουργία ισχύος

Το x a με θετικό εκθέτη a μεγαλώνει ταχύτερα από τον λογάριθμο.

Ιδιότητες του φυσικού λογάριθμου

Τομέας ορισμού, σύνολο τιμών, άκρα, αύξηση, μείωση

Ο φυσικός λογάριθμος είναι μια μονότονα αυξανόμενη συνάρτηση, επομένως δεν έχει ακρότατα. Οι κύριες ιδιότητες του φυσικού λογάριθμου παρουσιάζονται στον πίνακα.

ln x τιμές

ln 1 = 0

Βασικοί τύποι για φυσικούς λογάριθμους

Τύποι που προκύπτουν από τον ορισμό της αντίστροφης συνάρτησης:

Η κύρια ιδιότητα των λογαρίθμων και οι συνέπειές της

Φόρμουλα αντικατάστασης βάσης

Οποιοσδήποτε λογάριθμος μπορεί να εκφραστεί με όρους φυσικών λογαρίθμων χρησιμοποιώντας τον τύπο αντικατάστασης βάσης:

Οι αποδείξεις αυτών των τύπων παρουσιάζονται στην ενότητα "Λογάριθμος".

Αντίστροφη συνάρτηση

Το αντίστροφο του φυσικού λογάριθμου είναι ο εκθέτης.

Αν τότε

Αν τότε.

Παράγωγο ln x
.
Παράγωγο του φυσικού λογάριθμου:
.
Παράγωγος του φυσικού λογάριθμου του συντελεστή x:
.
Παράγωγο νης τάξης:

Εξαγωγή τύπων > > >

Αναπόσπαστο
.
Το ολοκλήρωμα υπολογίζεται με ολοκλήρωση ανά μέρη:

Ετσι,

Εκφράσεις με χρήση μιγαδικών αριθμών
.
Εξετάστε τη συνάρτηση της μιγαδικής μεταβλητής z: Ας εκφράσουμε τη σύνθετη μεταβλητή z μέσω ενότητας r φ :
.
και επιχείρημα
.
Χρησιμοποιώντας τις ιδιότητες του λογάριθμου, έχουμε:
.
Ή
Το όρισμα φ δεν ορίζεται μοναδικά. Αν βάλεις
, όπου n είναι ακέραιος,

θα είναι ο ίδιος αριθμός για διαφορετικά n.

Επομένως, ο φυσικός λογάριθμος, ως συνάρτηση μιας μιγαδικής μεταβλητής, δεν είναι συνάρτηση μίας τιμής.

Επέκταση σειράς ισχύος

Όταν πραγματοποιείται η επέκταση:
Βιβλιογραφικές αναφορές:

ΣΕ. Bronstein, Κ.Α. Semendyaev, Εγχειρίδιο μαθηματικών για μηχανικούς και φοιτητές, "Lan", 2009.

\(a^(b)=c\) \(\αριστερό βέλος\) \(\log_(a)(c)=b\)

Ας το εξηγήσουμε πιο απλά. Για παράδειγμα, το \(\log_(2)(8)\) ισούται με την ισχύ στην οποία πρέπει να αυξηθεί το \(2\) για να ληφθεί \(8\). Από αυτό είναι σαφές ότι \(\log_(2)(8)=3\).

Παραδείγματα:

\(\log_(5)(25)=2\)

επειδή \(5^(2)=25\)

\(\log_(3)(81)=4\)

επειδή \(3^(4)=81\)

\(\log_(2)\)\(\frac(1)(32)\) \(=-5\)

επειδή \(2^(-5)=\)\(\frac(1)(32)\)

Οποιοσδήποτε λογάριθμος έχει την ακόλουθη «ανατομία»:

Το όρισμα ενός λογάριθμου γράφεται συνήθως στο επίπεδό του και η βάση γράφεται σε δείκτη πιο κοντά στο πρόσημο του λογάριθμου. Και αυτό το λήμμα έχει ως εξής: «λογάριθμος του είκοσι πέντε στη βάση του πέντε».

Πώς να υπολογίσετε τον λογάριθμο;

Για να υπολογίσετε τον λογάριθμο, πρέπει να απαντήσετε στην ερώτηση: σε ποια δύναμη πρέπει να ανυψωθεί η βάση για να ληφθεί το όρισμα;

Για παράδειγμα, υπολογίστε τον λογάριθμο: α) \(\log_(4)(16)\) β) \(\log_(3)\)\(\frac(1)(3)\) γ) \(\log_(\ sqrt (5))(1)\) δ) \(\log_(\sqrt(7))(\sqrt(7))\) e) \(\log_(3)(\sqrt(3))\)

α) Σε ποια δύναμη πρέπει να ανυψωθεί το \(4\) για να πάρει το \(16\); Προφανώς το δεύτερο. Να γιατί:

\(\log_(4)(16)=2\)

\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)

γ) Σε ποια δύναμη πρέπει να αυξηθεί το \(\sqrt(5)\) για να ληφθεί το \(1\); Ποια δύναμη κάνει οποιοδήποτε νούμερο ένα; Μηδέν, φυσικά!

\(\log_(\sqrt(5))(1)=0\)

δ) Σε ποια δύναμη πρέπει να αυξηθεί το \(\sqrt(7)\) για να ληφθεί το \(\sqrt(7)\); Πρώτον, οποιοσδήποτε αριθμός στην πρώτη δύναμη είναι ίσος με τον εαυτό του.

\(\log_(\sqrt(7))(\sqrt(7))=1\)

ε) Σε ποια δύναμη πρέπει να αυξηθεί το \(3\) για να ληφθεί \(\sqrt(3)\); Από γνωρίζουμε ότι είναι μια κλασματική δύναμη, που σημαίνει Τετραγωνική ρίζαείναι η δύναμη του \(\frac(1)(2)\) .

\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)

Παράδειγμα : Υπολογισμός λογάριθμου \(\log_(4\sqrt(2))(8)\)

Λύση :

\(\log_(4\sqrt(2))(8)=x\)

Πρέπει να βρούμε την τιμή του λογάριθμου, ας τη συμβολίσουμε ως x. Τώρα ας χρησιμοποιήσουμε τον ορισμό του λογάριθμου:
\(\log_(a)(c)=b\) \(\αριστερό βέλος\) \(a^(b)=c\)

\((4\sqrt(2))^(x)=8\)

Τι συνδέει τα \(4\sqrt(2)\) και \(8\); Δύο, επειδή και οι δύο αριθμοί μπορούν να αναπαρασταθούν με δύο:
\(4=2^(2)\) \(\sqrt(2)=2^(\frac(1)(2))\) \(8=2^(3)\)

\(((2^(2)\cdot2^(\frac(1)(2))))^(x)=2^(3)\)

Στα αριστερά χρησιμοποιούμε τις ιδιότητες του βαθμού: \(a^(m)\cdot a^(n)=a^(m+n)\) και \((a^(m))^(n)= a^(m\cdot n)\)

\(2^(\frac(5)(2)x)=2^(3)\)

Οι βάσεις είναι ίσες, προχωράμε στην ισότητα των δεικτών

\(\frac(5x)(2)\) \(=3\)

Πολλαπλασιάστε και τις δύο πλευρές της εξίσωσης με \(\frac(2)(5)\)

Η ρίζα που προκύπτει είναι η τιμή του λογάριθμου

Απάντηση : \(\log_(4\sqrt(2))(8)=1,2\)

Γιατί εφευρέθηκε ο λογάριθμος;

Για να το καταλάβουμε αυτό, ας λύσουμε την εξίσωση: \(3^(x)=9\). Απλώς αντιστοιχίστε το \(x\) για να λειτουργήσει η ισότητα. Φυσικά, \(x=2\).

Λύστε τώρα την εξίσωση: \(3^(x)=8\).Με τι ισούται το x; Αυτό είναι το νόημα.

Οι πιο έξυπνοι θα πουν: «Το Χ είναι λίγο λιγότερο από δύο». Πώς ακριβώς γράφεται αυτός ο αριθμός; Για να απαντηθεί αυτή η ερώτηση, εφευρέθηκε ο λογάριθμος. Χάρη σε αυτόν, η απάντηση εδώ μπορεί να γραφτεί ως \(x=\log_(3)(8)\).

Θέλω να τονίσω ότι \(\log_(3)(8)\), όπως οποιοσδήποτε λογάριθμος είναι απλώς ένας αριθμός. Ναι, φαίνεται ασυνήθιστο, αλλά είναι σύντομο. Γιατί αν θέλαμε να το γράψουμε ως δεκαδικό, θα έμοιαζε κάπως έτσι: \(1.892789260714.....\)

Παράδειγμα : Λύστε την εξίσωση \(4^(5x-4)=10\)

Λύση :

\(4^(5x-4)=10\)

Τα \(4^(5x-4)\) και \(10\) δεν μπορούν να μεταφερθούν στην ίδια βάση. Αυτό σημαίνει ότι δεν μπορείτε να κάνετε χωρίς λογάριθμο.

Ας χρησιμοποιήσουμε τον ορισμό του λογάριθμου:
\(a^(b)=c\) \(\αριστερό βέλος\) \(\log_(a)(c)=b\)

\(\log_(4)(10)=5x-4\)

Ας αναστρέψουμε την εξίσωση έτσι ώστε το Χ να βρίσκεται στα αριστερά

\(5x-4=\log_(4)(10)\)

Πριν από εμάς. Ας μετακινηθούμε \(4\) προς τα δεξιά.

Και μην φοβάστε τον λογάριθμο, αντιμετώπισέ τον σαν έναν συνηθισμένο αριθμό.

\(5x=\log_(4)(10)+4\)

Διαιρέστε την εξίσωση με το 5

\(x=\)\(\frac(\log_(4)(10)+4)(5)\)

Αυτή είναι η ρίζα μας. Ναι, φαίνεται ασυνήθιστο, αλλά δεν επιλέγουν την απάντηση.

Απάντηση : \(\frac(\log_(4)(10)+4)(5)\)

Δεκαδικοί και φυσικοί λογάριθμοι

Όπως αναφέρεται στον ορισμό ενός λογάριθμου, η βάση του μπορεί να είναι οποιοσδήποτε θετικός αριθμός εκτός από ένα \((a>0, a\neq1)\). Και μεταξύ όλων των πιθανών βάσεων, υπάρχουν δύο που εμφανίζονται τόσο συχνά που εφευρέθηκε μια ειδική σύντομη σημειογραφία για τους λογάριθμους με αυτές:

Φυσικός λογάριθμος: ένας λογάριθμος του οποίου η βάση είναι ο αριθμός του Euler \(e\) (ίσος με περίπου \(2.7182818…\)), και ο λογάριθμος γράφεται ως \(\ln(a)\).

Αυτό είναι, Το \(\ln(a)\) είναι το ίδιο με το \(\log_(e)(a)\)

Δεκαδικός λογάριθμος: Ένας λογάριθμος του οποίου η βάση είναι 10 γράφεται \(\lg(a)\).

Αυτό είναι, Το \(\lg(a)\) είναι το ίδιο με το \(\log_(10)(a)\), όπου \(a\) είναι κάποιος αριθμός.

Βασική λογαριθμική ταυτότητα

Οι λογάριθμοι έχουν πολλές ιδιότητες. Ένα από αυτά ονομάζεται «Βασική Λογαριθμική Ταυτότητα» και μοιάζει με αυτό:

\(a^(\log_(a)(c))=c\)

Αυτή η ιδιότητα προκύπτει άμεσα από τον ορισμό. Ας δούμε πώς ακριβώς προέκυψε αυτή η φόρμουλα.

Ας θυμηθούμε μια σύντομη σημειογραφία του ορισμού του λογάριθμου:

αν \(a^(b)=c\), τότε \(\log_(a)(c)=b\)

Δηλαδή, το \(b\) είναι το ίδιο με το \(\log_(a)(c)\). Τότε μπορούμε να γράψουμε \(\log_(a)(c)\) αντί για \(b\) στον τύπο \(a^(b)=c\). Αποδείχθηκε \(a^(\log_(a)(c))=c\) - η κύρια λογαριθμική ταυτότητα.

Μπορείτε να βρείτε άλλες ιδιότητες των λογαρίθμων. Με τη βοήθειά τους, μπορείτε να απλοποιήσετε και να υπολογίσετε τις τιμές των παραστάσεων με λογάριθμους, οι οποίοι είναι δύσκολο να υπολογιστούν άμεσα.

Παράδειγμα : Βρείτε την τιμή της παράστασης \(36^(\log_(6)(5))\)

Λύση :

Απάντηση : \(25\)

Πώς να γράψετε έναν αριθμό ως λογάριθμο;

Όπως αναφέρθηκε παραπάνω, οποιοσδήποτε λογάριθμος είναι απλώς ένας αριθμός. Το αντίστροφο ισχύει επίσης: οποιοσδήποτε αριθμός μπορεί να γραφτεί ως λογάριθμος. Για παράδειγμα, γνωρίζουμε ότι το \(\log_(2)(4)\) είναι ίσο με δύο. Στη συνέχεια, μπορείτε να γράψετε \(\log_(2)(4)\) αντί για δύο.

Αλλά το \(\log_(3)(9)\) είναι επίσης ίσο με \(2\), που σημαίνει ότι μπορούμε επίσης να γράψουμε \(2=\log_(3)(9)\) . Ομοίως με το \(\log_(5)(25)\), και με το \(\log_(9)(81)\), κ.λπ. Δηλαδή αποδεικνύεται

\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)

Έτσι, αν χρειαζόμαστε, μπορούμε να γράψουμε δύο ως λογάριθμο με οποιαδήποτε βάση οπουδήποτε (είτε σε μια εξίσωση, σε μια έκφραση ή σε μια ανισότητα) - γράφουμε απλώς τη βάση στο τετράγωνο ως όρισμα.

Είναι το ίδιο με το τριπλό – μπορεί να γραφτεί ως \(\log_(2)(8)\), ή ως \(\log_(3)(27)\), ή ως \(\log_(4)( 64) \)... Εδώ γράφουμε τη βάση στον κύβο ως όρισμα:

\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)

Και με τέσσερα:

\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)

Και με μείον ένα:

\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1 )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1)(7)\) \(...\)

Και με το ένα τρίτο:

\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)

Οποιοσδήποτε αριθμός \(a\) μπορεί να αναπαρασταθεί ως λογάριθμος με βάση \(b\): \(a=\log_(b)(b^(a))\)

Παράδειγμα : Βρείτε το νόημα της έκφρασης \(\frac(\log_(2)(14))(1+\log_(2)(7))\)

Λύση :

Απάντηση : \(1\)

Ορισμός λογάριθμου

Ο λογάριθμος του b στη βάση του a είναι ο εκθέτης στον οποίο πρέπει να αυξηθεί το a για να ληφθεί το b.

Αριθμός εστα μαθηματικά συνηθίζεται να δηλώνεται το όριο στο οποίο αγωνίζεται μια έκφραση

Αριθμός εείναι παράλογος αριθμός- ένας αριθμός ασύμμετρος με ένα, δεν μπορεί να εκφραστεί με ακρίβεια ούτε ως ακέραιος ούτε ως κλάσμα λογικόςαριθμός.

Γράμμα μι- το πρώτο γράμμα μιας λατινικής λέξης εκθέτης- για επίδειξη, εξ ου και το όνομα στα μαθηματικά εκθετικός- εκθετικη συναρτηση.

Αριθμός μιχρησιμοποιείται ευρέως στα μαθηματικά και σε όλες τις επιστήμες που με τον ένα ή τον άλλο τρόπο χρησιμοποιούν μαθηματικούς υπολογισμούς για τις ανάγκες τους.

Λογάριθμοι. Ιδιότητες λογαρίθμων

Ορισμός: Ο λογάριθμος ενός θετικού αριθμού b στη βάση του είναι ο εκθέτης c στον οποίο πρέπει να αυξηθεί ο αριθμός a για να ληφθεί ο αριθμός b.

Βασική λογαριθμική ταυτότητα:

7) Φόρμουλα για μετάβαση σε νέα βάση:

lna = log e a, e ≈ 2,718…

Προβλήματα και τεστ με θέμα «Λογάριθμοι. Ιδιότητες των λογαρίθμων"

  • Λογάριθμοι - Σημαντικά θέματα για την ανασκόπηση της Ενιαίας Κρατικής Εξέτασης στα μαθηματικά

Για να ολοκληρώσετε επιτυχώς εργασίες σε αυτό το θέμα, πρέπει να γνωρίζετε τον ορισμό ενός λογαρίθμου, τις ιδιότητες των λογαρίθμων, τη βασική λογαριθμική ταυτότητα, τους ορισμούς των δεκαδικών και φυσικών λογαρίθμων. Οι κύριοι τύποι προβλημάτων σε αυτό το θέμα είναι προβλήματα που αφορούν τον υπολογισμό και τον μετασχηματισμό λογαριθμικών παραστάσεων. Ας εξετάσουμε τη λύση τους χρησιμοποιώντας τα ακόλουθα παραδείγματα.

Λύση:Χρησιμοποιώντας τις ιδιότητες των λογαρίθμων, παίρνουμε

Λύση:Χρησιμοποιώντας τις ιδιότητες των βαθμών, παίρνουμε

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Ιδιότητες λογαρίθμων, διατυπώσεις και αποδείξεις.

Οι λογάριθμοι έχουν έναν αριθμό από χαρακτηριστικές ιδιότητες. Σε αυτό το άρθρο θα δούμε τα κύρια ιδιότητες των λογαρίθμων. Εδώ θα δώσουμε τις διατυπώσεις τους, θα καταγράψουμε τις ιδιότητες των λογαρίθμων με τη μορφή τύπων, θα δείξουμε παραδείγματα της εφαρμογής τους και θα παράσχουμε επίσης απόδειξη των ιδιοτήτων των λογαρίθμων.

Πλοήγηση στη σελίδα.

Βασικές ιδιότητες λογαρίθμων, τύποι

Για ευκολία στη μνήμη και στη χρήση, ας φανταστούμε βασικές ιδιότητες των λογαρίθμωνμε τη μορφή λίστας τύπων. Στην επόμενη παράγραφο θα δώσουμε τις διατυπώσεις τους, στοιχεία, παραδείγματα χρήσης και απαραίτητες εξηγήσεις.

  • Ιδιότητα του λογάριθμου της ενότητας: log a 1=0 για κάθε a>0, a≠1.
  • Λογάριθμος αριθμού ίσου με τη βάση: log a a=1 για a>0, a≠1.
  • Ιδιότητα του λογάριθμου της ισχύος της βάσης: log a a p =p, όπου a>0, a≠1 και p είναι οποιοσδήποτε πραγματικός αριθμός.
  • Λογάριθμος του γινόμενου δύο θετικών αριθμών: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
    και η ιδιότητα του λογάριθμου του γινομένου n θετικών αριθμών: log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x 2 >0, …, x n >0 .
  • Ιδιότητα του λογάριθμου ενός πηλίκου: , όπου a>0, a≠1, x>0, y>0.
  • Λογάριθμος της ισχύος ενός αριθμού: log a b p =p·log a |b| , όπου a>0, a≠1, b και p είναι αριθμοί τέτοιοι ώστε ο βαθμός b p έχει νόημα και b p >0.
  • Συνέπεια: , όπου a>0, a≠1, n είναι φυσικός αριθμός μεγαλύτερος του ενός, b>0.
  • Συμπέρασμα 1: , a>0 , a≠1 , b>0 , b≠1 .
  • Συμπέρασμα 2: , a>0 , a≠1 , b>0 , p και q είναι πραγματικοί αριθμοί, q≠0 , συγκεκριμένα για b=a έχουμε .

    • Συνθέσεις και αποδείξεις ιδιοτήτων

    Προχωράμε στη διατύπωση και απόδειξη των γραπτών ιδιοτήτων των λογαρίθμων. Όλες οι ιδιότητες των λογαρίθμων αποδεικνύονται με βάση τον ορισμό του λογαρίθμου και τη βασική λογαριθμική ταυτότητα που προκύπτει από αυτόν, καθώς και τις ιδιότητες του βαθμού.

    Ας ξεκινήσουμε με ιδιότητες του λογάριθμου του ενός. Η διατύπωσή του έχει ως εξής: ο λογάριθμος της ενότητας είναι ίσος με μηδέν, δηλαδή καταγράψτε ένα 1=0για οποιοδήποτε a>0, a≠1. Η απόδειξη δεν είναι δύσκολη: αφού ένα 0 =1 για οποιοδήποτε a ικανοποιεί τις παραπάνω συνθήκες a>0 και a≠1, τότε το log ισότητας a 1=0 που πρέπει να αποδειχθεί προκύπτει αμέσως από τον ορισμό του λογαρίθμου.

    Ας δώσουμε παραδείγματα εφαρμογής της εξεταζόμενης ιδιότητας: log 3 1=0, log1=0 και .

    Ας προχωρήσουμε στο επόμενο ακίνητο: ο λογάριθμος ενός αριθμού ίσου με τη βάση είναι ίσος με ένα, αυτό είναι, καταγραφή a a=1για a>0, a≠1. Πράγματι, εφόσον a 1 =a για οποιοδήποτε a, τότε εξ ορισμού του λογαρίθμου log a a=1.

    Παραδείγματα χρήσης αυτής της ιδιότητας των λογαρίθμων είναι οι ισότητες log 5 5=1, log 5.6 5.6 και lne=1.

    Ο λογάριθμος ισχύος ενός αριθμού ίσου με τη βάση του λογαρίθμου είναι ίσος με τον εκθέτη. Αυτή η ιδιότητα του λογαρίθμου αντιστοιχεί σε έναν τύπο της μορφής log a a p =p, όπου a>0, a≠1 και p – οποιοσδήποτε πραγματικός αριθμός. Αυτή η ιδιότητα προκύπτει άμεσα από τον ορισμό του λογάριθμου. Σημειώστε ότι σας επιτρέπει να υποδείξετε αμέσως την τιμή του λογαρίθμου, εάν είναι δυνατό να αναπαραστήσετε τον αριθμό κάτω από το σύμβολο του λογαρίθμου ως δύναμη της βάσης, θα μιλήσουμε περισσότερα για αυτό στο άρθρο υπολογισμού λογαρίθμων.

    Για παράδειγμα, log 2 2 7 =7, log10 -4 =-4 και .

    Λογάριθμος του γινομένου δύο θετικών αριθμών x και y είναι ίσο με το γινόμενο των λογαρίθμων αυτών των αριθμών: log a (x y)=log a x+log a y, a>0 , a≠1 . Ας αποδείξουμε την ιδιότητα του λογάριθμου ενός γινομένου. Λόγω των ιδιοτήτων του βαθμού a log a x+log a y =a log a x ·a log a y, και εφόσον από την κύρια λογαριθμική ταυτότητα ένα log a x =x και ένα log a y =y, τότε ένα log a x ·a log a y =x· y. Έτσι, ένα log a x+log a y =x·y, από το οποίο, με τον ορισμό ενός λογάριθμου, προκύπτει η ισότητα που αποδεικνύεται.

    Ας δείξουμε παραδείγματα χρήσης της ιδιότητας του λογάριθμου ενός προϊόντος: log 5 (2 3)=log 5 2+log 5 3 και .

    Η ιδιότητα του λογάριθμου ενός γινομένου μπορεί να γενικευτεί στο γινόμενο ενός πεπερασμένου αριθμού n θετικών αριθμών x 1 , x 2 , …, x n ως log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n. Αυτή η ισότητα μπορεί να αποδειχθεί χωρίς προβλήματα χρησιμοποιώντας τη μέθοδο της μαθηματικής επαγωγής.

    Για παράδειγμα, ο φυσικός λογάριθμος του γινομένου μπορεί να αντικατασταθεί από το άθροισμα τριών φυσικών λογαρίθμων των αριθμών 4, e και.

    Λογάριθμος του πηλίκου δύο θετικών αριθμώνΤο x και το y είναι ίσο με τη διαφορά μεταξύ των λογαρίθμων αυτών των αριθμών. Η ιδιότητα του λογάριθμου ενός πηλίκου αντιστοιχεί σε έναν τύπο της μορφής , όπου a>0, a≠1, x και y είναι κάποιοι θετικοί αριθμοί. Η εγκυρότητα αυτού του τύπου αποδεικνύεται καθώς και ο τύπος για τον λογάριθμο ενός προϊόντος: αφού , τότε εξ ορισμού του λογάριθμου .

    Ακολουθεί ένα παράδειγμα χρήσης αυτής της ιδιότητας του λογάριθμου: .

    Ας προχωρήσουμε στο ιδιότητα του λογάριθμου της ισχύος. Ο λογάριθμος μιας μοίρας είναι ίσος με το γινόμενο του εκθέτη και το λογάριθμο του συντελεστή μέτρησης της βάσης αυτού του βαθμού. Ας γράψουμε αυτή την ιδιότητα του λογάριθμου μιας δύναμης ως τύπο: log a b p =p·log a |b|, όπου a>0, a≠1, b και p είναι αριθμοί τέτοιοι ώστε ο βαθμός b p έχει νόημα και b p >0.

    Αρχικά αποδεικνύουμε αυτή την ιδιότητα ως θετική β. Η βασική λογαριθμική ταυτότητα μας επιτρέπει να αναπαραστήσουμε τον αριθμό b ως log a b , μετά b p =(a log a b) p , και η παράσταση που προκύπτει, λόγω της ιδιότητας της ισχύος, είναι ίση με a p·log a b . Άρα καταλήγουμε στην ισότητα b p =a p·log a b, από την οποία, με τον ορισμό ενός λογάριθμου, συμπεραίνουμε ότι log a b p =p·log a b.

    Μένει να αποδειχθεί αυτή η ιδιότητα για αρνητικό β. Εδώ σημειώνουμε ότι η έκφραση log a b p για αρνητικό b έχει νόημα μόνο για άρτιους εκθέτες p (καθώς η τιμή του βαθμού b p πρέπει να είναι μεγαλύτερη από το μηδέν, διαφορετικά ο λογάριθμος δεν θα έχει νόημα), και σε αυτή την περίπτωση b p =|b| Π. Τότε b p =|b| p =(a log a |b|) p =a p·log a |b| , από όπου log a b p =p·log a |b| .

    Για παράδειγμα, και ln(-3) 4 =4·ln|-3|=4·ln3 .

    Προκύπτει από το προηγούμενο ακίνητο ιδιότητα του λογάριθμου από τη ρίζα: ο λογάριθμος της νης ρίζας είναι ίσος με το γινόμενο του κλάσματος 1/n με το λογάριθμο της ριζικής έκφρασης, δηλαδή όπου a>0, a≠1, n είναι φυσικός αριθμός μεγαλύτερος του ενός, b>0 .

    Η απόδειξη βασίζεται στην ισότητα (βλ. ορισμό εκθέτη με κλασματικό εκθέτη), που ισχύει για κάθε θετικό b, και στην ιδιότητα του λογάριθμου του εκθέτη: .

    Ακολουθεί ένα παράδειγμα χρήσης αυτής της ιδιότητας: .

    Τώρα ας αποδείξουμε τύπος για μετάβαση σε νέα βάση λογαρίθμουείδος . Για να γίνει αυτό, αρκεί να αποδείξουμε την εγκυρότητα του log ισότητας c b=log a b·log c a. Η βασική λογαριθμική ταυτότητα μας επιτρέπει να αναπαραστήσουμε τον αριθμό b ως log a b , μετά το log c b=log c a log a b . Απομένει να χρησιμοποιήσουμε την ιδιότητα του λογάριθμου του βαθμού: log c a log a b =log a b·log c a . Αυτό αποδεικνύει την ισότητα log c b=log a b·log c a, που σημαίνει ότι αποδεικνύεται και ο τύπος για τη μετάβαση σε μια νέα βάση του λογαρίθμου .

    Ας δείξουμε μερικά παραδείγματα χρήσης αυτής της ιδιότητας των λογαρίθμων: και .

    Ο τύπος για τη μετάβαση σε μια νέα βάση σάς επιτρέπει να προχωρήσετε στην εργασία με λογάριθμους που έχουν «βολική» βάση. Για παράδειγμα, μπορεί να χρησιμοποιηθεί για αλλαγή σε φυσικούς ή δεκαδικούς λογάριθμους, ώστε να μπορείτε να υπολογίσετε την τιμή ενός λογαρίθμου από έναν πίνακα λογαρίθμων. Ο τύπος για τη μετάβαση σε μια νέα βάση λογαρίθμου επιτρέπει επίσης, σε ορισμένες περιπτώσεις, να βρεθεί η τιμή ενός δεδομένου λογαρίθμου όταν είναι γνωστές οι τιμές ορισμένων λογαρίθμων με άλλες βάσεις.

    Συχνά χρησιμοποιείται μια ειδική περίπτωση του τύπου για μετάβαση σε νέα βάση λογαρίθμου για c=b της φόρμας. Αυτό δείχνει ότι το log a b και το log b a είναι αμοιβαία αντίστροφοι αριθμοί. Π.χ, .

    Ο τύπος χρησιμοποιείται επίσης συχνά, ο οποίος είναι βολικός για την εύρεση των τιμών των λογαρίθμων. Για να επιβεβαιώσουμε τα λόγια μας, θα δείξουμε πώς μπορεί να χρησιμοποιηθεί για τον υπολογισμό της τιμής ενός λογάριθμου της φόρμας . Εχουμε . Για να αποδείξετε τον τύπο, αρκεί να χρησιμοποιήσετε τον τύπο για τη μετάβαση σε μια νέα βάση του λογάριθμου α: .

    Μένει να αποδείξουμε τις ιδιότητες σύγκρισης των λογαρίθμων.

    Ας χρησιμοποιήσουμε την αντίθετη μέθοδο. Ας υποθέσουμε ότι για 1 >1, a 2 >1 και a 1 2 και για 0 ​​1, log a 1 b≤log a 2 b είναι αληθές. Με βάση τις ιδιότητες των λογαρίθμων, αυτές οι ανισότητες μπορούν να ξαναγραφτούν ως Και αντίστοιχα, και από αυτά προκύπτει ότι το log b a 1 ≤log b a 2 και το log b a 1 ≥log b a 2, αντίστοιχα. Τότε, σύμφωνα με τις ιδιότητες των δυνάμεων με τις ίδιες βάσεις, πρέπει να ισχύουν οι ισότητες b log b a 1 ≥b log b a 2 και b log b a 1 ≥b log b a 2, δηλαδή a 1 ≥a 2 . Έτσι καταλήξαμε σε μια αντίφαση με την συνθήκη a 1 2. Αυτό συμπληρώνει την απόδειξη.

    Βασικές ιδιότητες των λογαρίθμων

    • Υλικά για το μάθημα
    • Κατεβάστε όλους τους τύπους

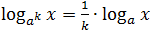
      • Οι λογάριθμοι, όπως κάθε αριθμός, μπορούν να προστεθούν, να αφαιρεθούν και να μετασχηματιστούν με κάθε τρόπο. Αλλά επειδή οι λογάριθμοι δεν είναι ακριβώς συνηθισμένοι αριθμοί, υπάρχουν κανόνες εδώ, οι οποίοι καλούνται κύριες ιδιότητες.

      Πρέπει οπωσδήποτε να γνωρίζετε αυτούς τους κανόνες - χωρίς αυτούς δεν μπορεί να λυθεί ούτε ένα σοβαρό λογαριθμικό πρόβλημα. Επιπλέον, υπάρχουν πολύ λίγα από αυτά - μπορείτε να μάθετε τα πάντα σε μια μέρα. Ας ξεκινήσουμε λοιπόν.

      Πρόσθεση και αφαίρεση λογαρίθμων

      Θεωρήστε δύο λογάριθμους με τις ίδιες βάσεις: log a x και log a y. Στη συνέχεια μπορούν να προστεθούν και να αφαιρεθούν και:

      Άρα, το άθροισμα των λογαρίθμων είναι ίσο με τον λογάριθμο του γινομένου και η διαφορά είναι ίση με τον λογάριθμο του πηλίκου. Παρακαλώ σημειώστε: το βασικό σημείο εδώ είναι πανομοιότυπους λόγους. Εάν οι λόγοι είναι διαφορετικοί, αυτοί οι κανόνες δεν λειτουργούν!

      Αυτοί οι τύποι θα σας βοηθήσουν να υπολογίσετε μια λογαριθμική παράσταση ακόμα και όταν δεν λαμβάνονται υπόψη τα επιμέρους μέρη της (δείτε το μάθημα «Τι είναι ο λογάριθμος»). Ρίξτε μια ματιά στα παραδείγματα και δείτε:

      Εργο. Βρείτε την τιμή της παράστασης: log 6 4 + log 6 9.

      Επειδή οι λογάριθμοι έχουν τις ίδιες βάσεις, χρησιμοποιούμε τον τύπο αθροίσματος:
      log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

      Εργο. Βρείτε την τιμή της παράστασης: log 2 48 − log 2 3.

      Οι βάσεις είναι ίδιες, χρησιμοποιούμε τον τύπο διαφοράς:
      log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

      Εργο. Βρείτε την τιμή της παράστασης: log 3 135 − log 3 5.

      Και πάλι οι βάσεις είναι ίδιες, οπότε έχουμε:
      log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

      Όπως μπορείτε να δείτε, οι αρχικές εκφράσεις αποτελούνται από «κακούς» λογάριθμους, οι οποίοι δεν υπολογίζονται χωριστά. Όμως μετά τους μετασχηματισμούς προκύπτουν εντελώς κανονικοί αριθμοί. Πολλά τεστ βασίζονται σε αυτό το γεγονός. Ναι, οι εκφράσεις που μοιάζουν με τεστ προσφέρονται με κάθε σοβαρότητα (μερικές φορές χωρίς σχεδόν καμία αλλαγή) στην Εξέταση Ενιαίου Κράτους.

      Εξαγωγή του εκθέτη από τον λογάριθμο

      Τώρα ας περιπλέκουμε λίγο το έργο. Τι γίνεται αν η βάση ή το όρισμα ενός λογαρίθμου είναι δύναμη; Τότε ο εκθέτης αυτού του βαθμού μπορεί να αφαιρεθεί από το πρόσημο του λογαρίθμου σύμφωνα με τους ακόλουθους κανόνες:

    • log a x n = n · log a x ;

      • Είναι εύκολο να δει κανείς ότι ο τελευταίος κανόνας ακολουθεί τους δύο πρώτους. Αλλά είναι καλύτερα να το θυμάστε ούτως ή άλλως - σε ορισμένες περιπτώσεις θα μειώσει σημαντικά τον όγκο των υπολογισμών.

      Φυσικά, όλοι αυτοί οι κανόνες έχουν νόημα αν παρατηρηθεί το ODZ του λογαρίθμου: a > 0, a ≠ 1, x > 0. Και κάτι ακόμα: μάθετε να εφαρμόζετε όλους τους τύπους όχι μόνο από αριστερά προς τα δεξιά, αλλά και αντίστροφα , δηλ. Μπορείτε να εισάγετε τους αριθμούς πριν από το σύμβολο του λογάριθμου στον ίδιο τον λογάριθμο. Αυτό είναι που απαιτείται συχνότερα.

      Εργο. Βρείτε την τιμή της παράστασης: log 7 49 6 .

      Ας απαλλαγούμε από το βαθμό στο όρισμα χρησιμοποιώντας τον πρώτο τύπο:
      log 7 49 6 = 6 log 7 49 = 6 2 = 12

      Εργο. Βρείτε το νόημα της έκφρασης:

      [Λεζάντα για την εικόνα]

      Σημειώστε ότι ο παρονομαστής περιέχει έναν λογάριθμο, η βάση και το όρισμα του οποίου είναι ακριβείς δυνάμεις: 16 = 2 4 ; 49 = 7 2. Εχουμε:

      [Λεζάντα για την εικόνα]

      Νομίζω ότι το τελευταίο παράδειγμα απαιτεί κάποια διευκρίνιση. Πού πήγαν οι λογάριθμοι; Μέχρι την τελευταία στιγμή δουλεύουμε μόνο με τον παρονομαστή. Παρουσιάσαμε τη βάση και το όρισμα του λογάριθμου που στέκεται εκεί με τη μορφή δυνάμεων και βγάλαμε τους εκθέτες - πήραμε ένα κλάσμα "τριώροφο".

      Τώρα ας δούμε το κύριο κλάσμα. Ο αριθμητής και ο παρονομαστής περιέχουν τον ίδιο αριθμό: log 2 7. Εφόσον το log 2 7 ≠ 0, μπορούμε να μειώσουμε το κλάσμα - τα 2/4 θα παραμείνουν στον παρονομαστή. Σύμφωνα με τους κανόνες της αριθμητικής, τα τέσσερα μπορούν να μεταφερθούν στον αριθμητή, πράγμα που έγινε. Το αποτέλεσμα ήταν η απάντηση: 2.

      Μετάβαση σε νέα βάση

      Μιλώντας για τους κανόνες πρόσθεσης και αφαίρεσης λογαρίθμων, τόνισα συγκεκριμένα ότι λειτουργούν μόνο με τις ίδιες βάσεις. Κι αν οι λόγοι είναι διαφορετικοί; Τι γίνεται αν δεν είναι ακριβείς δυνάμεις του ίδιου αριθμού;

      Οι φόρμουλες για τη μετάβαση σε ένα νέο θεμέλιο έρχονται στη διάσωση. Ας τα διατυπώσουμε με τη μορφή ενός θεωρήματος:

      Ας δοθεί το λογάριθμο log a x. Τότε για οποιονδήποτε αριθμό c τέτοιο ώστε c > 0 και c ≠ 1, η ισότητα είναι αληθής:

      [Λεζάντα για την εικόνα]

      Συγκεκριμένα, αν θέσουμε c = x, παίρνουμε:

      [Λεζάντα για την εικόνα]

      Από τον δεύτερο τύπο προκύπτει ότι η βάση και το όρισμα του λογάριθμου μπορούν να αντικατασταθούν, αλλά σε αυτήν την περίπτωση ολόκληρη η έκφραση "αναποδογυρίζεται", δηλ. ο λογάριθμος εμφανίζεται στον παρονομαστή.

      Αυτοί οι τύποι βρίσκονται σπάνια σε συνηθισμένες αριθμητικές εκφράσεις. Είναι δυνατό να αξιολογήσουμε πόσο βολικές είναι μόνο όταν λύνουμε λογαριθμικές εξισώσεις και ανισώσεις.

      Ωστόσο, υπάρχουν προβλήματα που δεν μπορούν να λυθούν καθόλου παρά μόνο με τη μετάβαση σε ένα νέο θεμέλιο. Ας δούμε μερικά από αυτά:

      Εργο. Βρείτε την τιμή της παράστασης: log 5 16 log 2 25.

      Σημειώστε ότι τα ορίσματα και των δύο λογαρίθμων περιέχουν ακριβείς δυνάμεις. Ας βγάλουμε τους δείκτες: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

      Τώρα ας «αντιστρέψουμε» τον δεύτερο λογάριθμο:

      [Λεζάντα για την εικόνα]

      Δεδομένου ότι το γινόμενο δεν αλλάζει κατά την αναδιάταξη των παραγόντων, πολλαπλασιάσαμε ήρεμα τέσσερα και δύο και στη συνέχεια ασχοληθήκαμε με τους λογάριθμους.

      Εργο. Βρείτε την τιμή της παράστασης: log 9 100 lg 3.

      Η βάση και το όρισμα του πρώτου λογάριθμου είναι ακριβείς δυνάμεις. Ας το γράψουμε αυτό και ας απαλλαγούμε από τους δείκτες:

      [Λεζάντα για την εικόνα]

      Τώρα ας απαλλαγούμε από τον δεκαδικό λογάριθμο μεταβαίνοντας σε μια νέα βάση:

      [Λεζάντα για την εικόνα]

      Βασική λογαριθμική ταυτότητα

      Συχνά στη διαδικασία επίλυσης είναι απαραίτητο να αναπαραστήσουμε έναν αριθμό ως λογάριθμο σε μια δεδομένη βάση. Σε αυτήν την περίπτωση, οι παρακάτω τύποι θα μας βοηθήσουν:

    1. n = log a a n

    2. Στην πρώτη περίπτωση, ο αριθμός n γίνεται ο εκθέτης στο όρισμα. Ο αριθμός n μπορεί να είναι απολύτως οτιδήποτε, γιατί είναι απλώς μια λογαριθμική τιμή.

      Ο δεύτερος τύπος είναι στην πραγματικότητα ένας παραφρασμένος ορισμός. Αυτό ονομάζεται: η βασική λογαριθμική ταυτότητα.

      Στην πραγματικότητα, τι συμβαίνει εάν ο αριθμός b αυξηθεί σε τέτοια δύναμη ώστε ο αριθμός b σε αυτή τη δύναμη να δώσει τον αριθμό a; Αυτό είναι σωστό: το αποτέλεσμα είναι ο ίδιος αριθμός α. Διαβάστε ξανά προσεκτικά αυτήν την παράγραφο - πολλοί άνθρωποι κολλάνε σε αυτήν.

      Όπως οι τύποι για τη μετάβαση σε μια νέα βάση, η βασική λογαριθμική ταυτότητα είναι μερικές φορές η μόνη δυνατή λύση.

      [Λεζάντα για την εικόνα]

      Σημειώστε ότι log 25 64 = log 5 8 - απλά πήραμε το τετράγωνο από τη βάση και το όρισμα του λογαρίθμου. Λαμβάνοντας υπόψη τους κανόνες για τον πολλαπλασιασμό των δυνάμεων με την ίδια βάση, παίρνουμε:

      [Λεζάντα για την εικόνα]

      Αν κάποιος δεν ξέρει, αυτή ήταν μια πραγματική εργασία από την Ενιαία Κρατική Εξέταση :)

      Λογαριθμική μονάδα και λογαριθμικό μηδέν

      Εν κατακλείδι, θα δώσω δύο ταυτότητες που δύσκολα μπορούν να ονομαστούν ιδιότητες - μάλλον είναι συνέπειες του ορισμού του λογαρίθμου. Εμφανίζονται συνεχώς σε προβλήματα και, παραδόξως, δημιουργούν προβλήματα ακόμη και σε «προχωρημένους» μαθητές.

      1. log a a = 1 είναι μια λογαριθμική μονάδα. Θυμηθείτε μια για πάντα: ο λογάριθμος σε οποιαδήποτε βάση α αυτής της ίδιας της βάσης είναι ίσος με ένα.
      2. log a 1 = 0 είναι λογαριθμικό μηδέν. Η βάση a μπορεί να είναι οτιδήποτε, αλλά αν το όρισμα περιέχει ένα, ο λογάριθμος είναι ίσος με μηδέν! Επειδή το 0 = 1 είναι άμεση συνέπεια του ορισμού.

      Αυτά είναι όλα τα ακίνητα. Φροντίστε να εξασκηθείτε στην εφαρμογή τους! Κατεβάστε το cheat sheet στην αρχή του μαθήματος, εκτυπώστε το και λύστε τα προβλήματα.

      Λογάριθμος. Ιδιότητες του λογάριθμου (πρόσθεση και αφαίρεση).

      Ιδιότητες του λογάριθμουαπό τον ορισμό του. Και έτσι ο λογάριθμος του αριθμού σιβασισμένο στο ΕΝΑορίζεται ως ο εκθέτης στον οποίο πρέπει να αυξηθεί ένας αριθμός έναγια να πάρετε τον αριθμό σι(ο λογάριθμος υπάρχει μόνο για θετικούς αριθμούς).

      Από τη διατύπωση αυτή προκύπτει ότι ο υπολογισμός x=log a β, ισοδυναμεί με την επίλυση της εξίσωσης a x =b.Για παράδειγμα, ημερολόγιο 2 8 = 3επειδή 8 = 2 3 . Η διατύπωση του λογαρίθμου καθιστά δυνατό να δικαιολογηθεί ότι αν b=a γ, τότε ο λογάριθμος του αριθμού σιβασισμένο στο έναισοδυναμεί Με. Είναι επίσης σαφές ότι το θέμα των λογαρίθμων σχετίζεται στενά με το θέμα των δυνάμεων.

      Με τους λογάριθμους, όπως και με όλους τους αριθμούς, μπορείτε να κάνετε πράξεις πρόσθεσης, αφαίρεσηςκαι μεταμορφώνονται με κάθε δυνατό τρόπο. Αλλά λόγω του γεγονότος ότι οι λογάριθμοι δεν είναι εντελώς συνηθισμένοι αριθμοί, εδώ ισχύουν οι δικοί τους ειδικοί κανόνες, οι οποίοι ονομάζονται κύριες ιδιότητες.

      Πρόσθεση και αφαίρεση λογαρίθμων.

      Ας πάρουμε δύο λογάριθμους με τις ίδιες βάσεις: καταγράψτε ένα xΚαι log a y. Στη συνέχεια, είναι δυνατή η εκτέλεση πράξεων πρόσθεσης και αφαίρεσης:

      Όπως βλέπουμε, άθροισμα λογαρίθμωνισούται με τον λογάριθμο του γινομένου, και διαφορά λογαρίθμων- λογάριθμος του πηλίκου. Επιπλέον, αυτό ισχύει αν οι αριθμοί ΕΝΑ, ΧΚαι στοθετικό και α ≠ 1.

      Είναι σημαντικό να σημειωθεί ότι η κύρια πτυχή σε αυτούς τους τύπους είναι οι ίδιες βάσεις. Εάν οι λόγοι είναι διαφορετικοί, αυτοί οι κανόνες δεν ισχύουν!

      Οι κανόνες για την πρόσθεση και την αφαίρεση λογαρίθμων με τις ίδιες βάσεις διαβάζονται όχι μόνο από αριστερά προς τα δεξιά, αλλά και αντίστροφα. Ως αποτέλεσμα, έχουμε τα θεωρήματα για τον λογάριθμο του γινομένου και τον λογάριθμο του πηλίκου.

      Λογάριθμος του προϊόντοςδύο θετικοί αριθμοί ίσο με το άθροισματους λογάριθμους τους ; αναδιατυπώνοντας αυτό το θεώρημα παίρνουμε το εξής αν οι αριθμοί ΕΝΑ, ΧΚαι στοθετικό και α ≠ 1, Οτι:

      Λογάριθμος του πηλίκουδύο θετικοί αριθμοί είναι ίσοι με τη διαφορά μεταξύ των λογαρίθμων του μερίσματος και του διαιρέτη. Για να το θέσω αλλιώς, αν οι αριθμοί ΕΝΑ, ΧΚαι στοθετικό και α ≠ 1, Οτι:

      Ας εφαρμόσουμε τα παραπάνω θεωρήματα για να λύσουμε παραδείγματα:

      Αν οι αριθμοί ΧΚαι στοείναι αρνητικά, λοιπόν τύπος λογάριθμου προϊόντοςγίνεται χωρίς νόημα. Έτσι, απαγορεύεται να γράψετε:

      αφού οι εκφράσεις log 2 (-8) και log 2 (-4) δεν ορίζονται καθόλου (λογαριθμική συνάρτηση στο= ημερολόγιο 2 Χορίζεται μόνο για θετικές τιμές ορίσματος Χ).

      Θεώρημα προϊόντοςισχύει όχι μόνο για δύο, αλλά και για απεριόριστο αριθμό παραγόντων. Αυτό σημαίνει ότι για κάθε φυσικό κκαι τυχόν θετικούς αριθμούς Χ 1 , Χ 2 , . . . ,x nυπάρχει ταυτότητα:

      Από θεώρημα λογαριθμικού πηλίκουμπορεί να ληφθεί μια ακόμη ιδιότητα του λογάριθμου. Είναι κοινό γνωστό ότι η καταγραφή ένα 1 = 0, επομένως

      Αυτό σημαίνει ότι υπάρχει ισότητα:

      Λογάριθμοι δύο αντίστροφων αριθμώνγια τον ίδιο λόγο θα διαφέρουν μεταξύ τους αποκλειστικά ως προς το πρόσημο. Ετσι:

      Λογάριθμος. Ιδιότητες λογαρίθμων

      Λογάριθμος. Ιδιότητες λογαρίθμων

      Ας εξετάσουμε την ισότητα. Ενημερώστε μας τις αξίες του και και θέλουμε να βρούμε την αξία του.

      Δηλαδή, αναζητούμε τον εκθέτη με τον οποίο πρέπει να τον οπλίσουμε για να πάρουμε .

      Αφήνω μια μεταβλητή μπορεί να λάβει οποιαδήποτε πραγματική τιμή, τότε επιβάλλονται οι ακόλουθοι περιορισμοί στις μεταβλητές: o" title="a>o"/> , 1″ title="a1″/>, 0″ title="b>0″ />

      Εάν γνωρίζουμε τις τιμές του και και βρισκόμαστε αντιμέτωποι με το καθήκον να βρούμε το άγνωστο, τότε για το σκοπό αυτό εισάγεται μια μαθηματική πράξη, η οποία ονομάζεται λογάριθμος.

      Για να βρούμε την τιμή που παίρνουμε λογάριθμος ενός αριθμούΜε βάση :

      Ο λογάριθμος ενός αριθμού στη βάση του είναι ο εκθέτης στον οποίο πρέπει να αυξηθεί για να ληφθεί .

      Αυτό είναι βασική λογαριθμική ταυτότητα:

      o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

      είναι ουσιαστικά μια μαθηματική σημειογραφία ορισμοί του λογάριθμου.

      Η μαθηματική πράξη του λογάριθμου είναι η αντίστροφη της πράξης της εκθέσεως, άρα ιδιότητες των λογαρίθμωνσχετίζονται στενά με τις ιδιότητες του πτυχίου.

      Ας παραθέσουμε τα κύρια ιδιότητες των λογαρίθμων:

      (o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

      d>0″/>, 1″ τίτλος=”d1″/>

      4.

      5.

      Η ακόλουθη ομάδα ιδιοτήτων σάς επιτρέπει να αναπαραστήσετε τον εκθέτη μιας έκφρασης κάτω από το πρόσημο του λογάριθμου ή να στέκεται στη βάση του λογαρίθμου με τη μορφή ενός συντελεστή μπροστά από το πρόσημο του λογαρίθμου:

      6.

      7.

      8.

      9.

      Η επόμενη ομάδα τύπων σας επιτρέπει να μετακινηθείτε από έναν λογάριθμο με δεδομένη βάση σε έναν λογάριθμο με αυθαίρετη βάση και ονομάζεται τύπους μετάβασης σε νέα βάση:

      10.

      12. (συμπέρασμα από την ιδιοκτησία 11)

      Οι ακόλουθες τρεις ιδιότητες δεν είναι πολύ γνωστές, αλλά χρησιμοποιούνται συχνά κατά την επίλυση λογαριθμικών εξισώσεων ή κατά την απλοποίηση παραστάσεων που περιέχουν λογάριθμους:

      13.

      14.

      15.

      Ειδικές περιπτώσεις:

      — δεκαδικός λογάριθμος

      — φυσικός λογάριθμος

      Όταν απλοποιούνται εκφράσεις που περιέχουν λογάριθμους, χρησιμοποιείται μια γενική προσέγγιση:

      1. Παρουσιάζοντας δεκαδικάμε τη μορφή των συνηθισμένων.

      2. Μικτά νούμεραπαριστάνονται ως ακατάλληλα κλάσματα.

      3. Αποσυνθέτουμε τους αριθμούς στη βάση του λογαρίθμου και κάτω από το πρόσημο του λογαρίθμου σε απλούς συντελεστές.

      4. Προσπαθούμε να ανάγουμε όλους τους λογάριθμους στην ίδια βάση.

      5. Εφαρμόστε τις ιδιότητες των λογαρίθμων.

      Ας δούμε παραδείγματα απλοποιητικών παραστάσεων που περιέχουν λογάριθμους.

      Παράδειγμα 1.

      Υπολογίζω:

      Ας απλοποιήσουμε όλους τους εκθέτες: το καθήκον μας είναι να τους αναγάγουμε σε λογάριθμους, η βάση των οποίων είναι ο ίδιος αριθμός με τη βάση του εκθέτη.

      ==(κατά ιδιότητα 7)=(κατά ιδιότητα 6) =

      Ας αντικαταστήσουμε τους δείκτες που πήραμε στην αρχική έκφραση. Παίρνουμε:

      Απάντηση: 5,25

      Παράδειγμα 2. Υπολογίστε:

      Ας μειώσουμε όλους τους λογάριθμους στη βάση 6 (σε αυτή την περίπτωση, οι λογάριθμοι από τον παρονομαστή του κλάσματος θα "μεταναστούν" στον αριθμητή):

      Ας αποσυνθέσουμε τους αριθμούς κάτω από το πρόσημο του λογαρίθμου σε απλούς παράγοντες:

      Ας εφαρμόσουμε τις ιδιότητες 4 και 6:

      Ας παρουσιάσουμε την αντικατάσταση

      Παίρνουμε:

      Απάντηση: 1

      Λογάριθμος . Βασική λογαριθμική ταυτότητα.

      Ιδιότητες λογαρίθμων. Δεκαδικός λογάριθμος. Φυσικός λογάριθμος.

      Λογάριθμος θετικός αριθμός N στη βάση (σι > 0, σι 1) είναι ο εκθέτης x στον οποίο πρέπει να αυξηθεί το b για να ληφθεί το N .

      Αυτή η καταχώρηση ισοδυναμεί με τα ακόλουθα: b x = N .

      Παραδείγματα: log 3 81 = 4, αφού 3 4 = 81;

      log 1/3 27 = – 3, αφού (1/3) - 3 = 3 3 = 27.

      Ο παραπάνω ορισμός του λογάριθμου μπορεί να γραφτεί ως ταυτότητα:

      Βασικές ιδιότητες των λογαρίθμων.

      2) log 1 = 0, αφού σι 0 = 1 .

      3) Ο λογάριθμος του γινομένου είναι ίσος με το άθροισμα των λογαρίθμων των παραγόντων:

      4) Ο λογάριθμος του πηλίκου είναι ίσος με τη διαφορά μεταξύ των λογαρίθμων του μερίσματος και του διαιρέτη:

      5) Ο λογάριθμος μιας ισχύος είναι ίσος με το γινόμενο του εκθέτη και του λογάριθμου της βάσης του:

      Το αποτέλεσμα αυτής της ιδιότητας είναι το εξής: λογάριθμος της ρίζας ίσο με το λογάριθμο του ριζικού αριθμού διαιρούμενο με τη δύναμη της ρίζας:

      6) Αν η βάση του λογαρίθμου είναι μια μοίρα, τότε η τιμή το αντίστροφο του εκθέτη μπορεί να ληφθεί ως ομοιοκαταληξία:

      Οι δύο τελευταίες ιδιότητες μπορούν να συνδυαστούν σε μία:

      7) Τύπος συντελεστή μετάβασης (δηλαδή μετάβαση από μια βάση λογαρίθμου σε μια άλλη βάση):

      Στην ειδική περίπτωση όταν N=aέχουμε:

      Δεκαδικός λογάριθμος που ονομάζεται λογάριθμος βάσης 10. Ονομάζεται lg, δηλ. ημερολόγιο 10 Ν= κούτσουρο Ν. Λογάριθμοι αριθμών 10, 100, 1000, . p είναι 1, 2, 3, …, αντίστοιχα, δηλ. έχουν τόσα θετικά

      μονάδες, πόσα μηδενικά υπάρχουν σε έναν λογαριθμικό αριθμό μετά το ένα. Λογάριθμοι αριθμών 0,1, 0,01, 0,001, . Τα p είναι αντίστοιχα –1, –2, –3, …, δηλ. έχουν τόσα αρνητικά όσα μηδενικά υπάρχουν στον λογαριθμικό αριθμό πριν από το ένα (συμπεριλαμβανομένων μηδενικών ακεραίων). Οι λογάριθμοι άλλων αριθμών έχουν ένα κλασματικό μέρος που ονομάζεται μάντισσα. Το ακέραιο μέρος ενός λογάριθμου ονομάζεται χαρακτηριστικό γνώρισμα. Για πρακτική χρήση, οι δεκαδικοί λογάριθμοι είναι πιο βολικοί.

      Φυσικός λογάριθμος που ονομάζεται λογάριθμος βάσης μι. Συμβολίζεται με ln, δηλ. κούτσουρο μι Ν= κούτσουρο Ν. Αριθμός μιείναι παράλογο, η κατά προσέγγιση τιμή του είναι 2,718281828. Είναι το όριο στο οποίο τείνει ο αριθμός (1 + 1 / n) nμε απεριόριστη αύξηση n(εκ. πρώτο υπέροχο όριοστη σελίδα "Όρια". ακολουθίες αριθμών»).
      Όσο παράξενο κι αν φαίνεται, οι φυσικοί λογάριθμοι αποδείχθηκαν πολύ βολικοί κατά την εκτέλεση διαφόρων τύπων πράξεων που σχετίζονται με την ανάλυση συναρτήσεων. Υπολογισμός λογαρίθμων στη βάση μιπραγματοποιείται πολύ πιο γρήγορα από οποιονδήποτε άλλο λόγο.